A/B 테스트 결과, 이게 맞아?
A/B 테스트 계산기, 믿어도 되는 걸까?
처음 A/B 테스트 결과 데이터를 받았을 때, ‘그래, 숫자는 나왔는데... 어떻게 분석해야 하지?’라는 고민이 생겼습니다. 찾아보니 A/B 테스트 계산기 사이트가 꽤 많더라고요. 처음 찾은 사이트는 이렇게 생겼습니다. 덕분에 A안과 B안의 차이가 유의미하다는 결과도 얻었고요. 다른 계산기 사이트들도 같은 결과를 내놓았습니다.
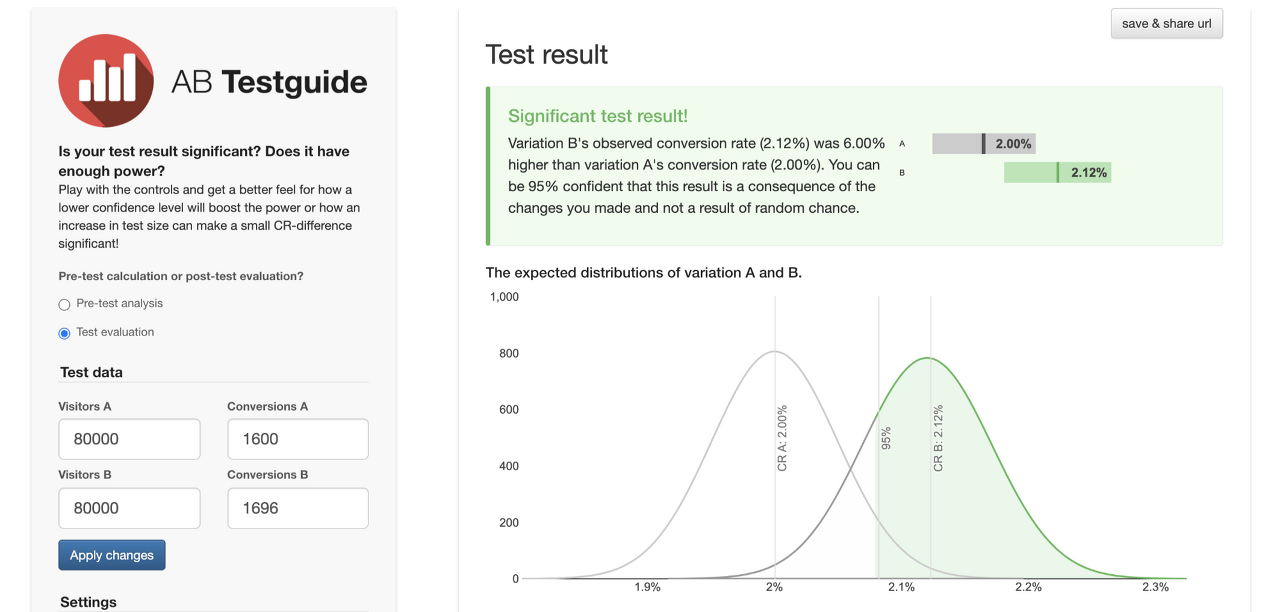
그런데 이 결과가 믿을만한 것인지 의심되었습니다. '사용자 수의 합계만 입력하는데, p-value까지 나오다니? 내가 대학원 때 했던 통계는 이리 간단하지 않았던 것 같은데, 과연 이 결과를 믿어도 될까?' 그래서 직접 검증하겠다고 마음을 먹었죠. 일이 이렇게 커질지 모르고 말이에요.
결론부터 말하면, A/B 테스트 계산기의 결과는 신뢰할 수 있습니다. 그러나 A/B 테스트 계산기의 결과를 어떻게 이해해야 하는지 아직 잘 모르겠다면 이 글이 도움이 될 거예요.
이 글은 A/B 테스트 검증 방법과 관련된 몇 가지 팁을 드립니다. 저는 처음에 전환율을 PV로 계산해야 하는지, UV로 계산해야 하는지부터 헷갈렸습니다. 그래서 측정 기준을 정하는 방법부터 시작해서 검증 방법까지 정리했습니다.
참고로 저는 통계 기초 지식이 부족해서 공부하면서 이 글을 썼습니다. 제가 다시 봐도 이해할 수 있도록 쉽게 썼으니 초보분들께도 도움이 될 것 같아요. 혹시나 오류를 발견하셨다면 댓글로 알려주시면 감사하겠습니다.
미국 실리콘밸리 인터넷 강의 사이트인 Udacity A/B Testing 강의에서 필요한 내용을 요약했고, 해당 강의를 파이썬 코드와 함께 더 자세하게 분석한 블로그 글을 참고했습니다. 본문에 수학 공식에 관한 내용도 있습니다. 혹시 설명이 부족하다면, Udacity 강의에서 더 자세히 들을 수 있습니다. A/B 테스트의 개념에 익숙하지 않은 분이라면, 기초적인 내용은 이 글에 잘 설명되어 있습니다.
※ 에디터 주 : Udacity 강의는 로그인 후 볼 수 있습니다.
1. 측정 기준 정하기
위 가설을 검증하기에 가장 적절한 측정 기준은 무엇일까요?
1-1. A/B 테스트에는 어떤 측정 기준이 있을까?
1) 버튼 클릭 건수
- 클릭 건수는 사용을 지양합니다.
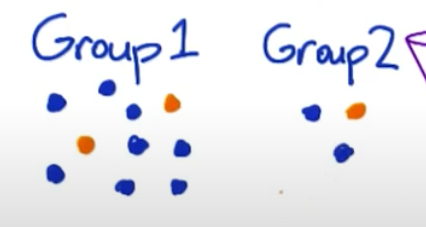
- 문제점: 아래 이미지를 참고해볼까요? 파란색은 홈페이지 접속 건수이고, 노란색은 홈페이지에서 버튼을 클릭한 건수입니다. Group 1은 홈페이지 접속 건수가 더 많기 때문에 버튼 클릭 건수도 더 많습니다. Group 2의 클릭 건수는 낮지만, 클릭 비율이 더 높습니다. 접속 건수가 많아서 클릭 건수가 많은 경우는 버튼의 효과로 인해 클릭 건수가 많아진 것이 아니므로 클릭 건수가 아닌 전환율을 측정합니다.
2) CTR(Click-through-rate) = 버튼 클릭 건수/홈페이지 접속 건수
- PV(Page View) 전환율을 사용하는 케이스입니다.
3) CTP(Click-through-probability) = 클릭한 Unique 사용자의 수/홈페이지에 접속한 Unique 사용자의 수
- UV(Unique Visitor) 전환율을 사용하는 케이스입니다.
- 한 번 이상 클릭한 사용자는 1, 한 번도 안 한 사용자는 0으로 계산합니다.
- 즉, 2명의 사용자 중 한 명은 0번 클릭하고, 한 명은 5번 클릭했을 때, CTR은 2.5(=(0+5)/2)이고, CTP는 0.5(=(0+1)/2)입니다.
1-2. A/B 테스트 측정 지표로 PV(CTR)을 사용해야 할까, UV(CTP)를 사용해야 할까?
1) 서비스의 사용성을 측정할 때는 PV를 사용합니다.
- 예를 들어, 특정 위치에 있는 버튼을 얼마나 자주 찾아서 누르는지 알고 싶을 때는 PV를 측정합니다.
2) 전체적인 영향을 측정할 때는 UV를 사용합니다.
- 예를 들어, 서비스의 다음 단계로 넘어가는 비율을 알고 싶을 때는 UV를 측정합니다.
- 페이지 로딩이 오래 걸려서 여러 번 클릭한 케이스 등을 제외해야 하기 때문입니다.
- 따라서 위에서 정한 가설은 서비스의 다음 단계로 넘어가는 비율을 알고자 하므로, UV(CTP)를 사용합니다.
2. B안을 선택할 근거는?
2-1. 측정 반복하기
어떤 사이트의 하루 동안 방문자가 1,000명입니다. 실험 1일 차에 버튼을 클릭한 방문자는 100명입니다. 이때 클릭한 방문자의 비율은 10%입니다.
실험 2일 차에 서비스 방문자 1,000명의 클릭 비율을 또 측정합니다. 이때 버튼을 클릭한 방문자 수가 몇 이상이면 놀랄 만할까요? 100명, 101명, 110명, 150명, 400명? 다시 말해서, 앞으로 시행을 반복했을 때 측정값이 얼마나 다양할지 알 방법이 있을까요? 그러려면 데이터의 분포를 알아야 합니다.
UV 전환율 측정 방법(CTP)은 연속된 값을 측정하지 않습니다. (연속된 값의 예: 키, 몸무게) 버튼을 클릭한다 =1, 버튼을 클릭하지 않는다=0의 두 가지 값만 측정하죠. 따라서 ‘이항 분포’를 따릅니다. 이항 분포를 따르는 것의 장점은, 이항 분포의 표준 오차 공식을 이용해 신뢰 구간을 계산할 수 있다는 것입니다.
2-2. 신뢰 구간(Confidence Intervals)
신뢰 구간은 모평균이 놓여 있을 것으로 자신하는 값의 구간입니다. 조금 더 풀어서 얘기해볼게요.
전체 사용자 10,000명을 모두 측정하기에는 시간과 돈이 많이 듭니다. 그래서 이 중 1,000명을 랜덤으로 뽑아서 전환율을 측정하기로 했습니다. 그런데 1,000명의 전환율이 10,000명의 전환율을 대표한다고 말할 수 있을까요? 여기서 10,000명을 모집단이라고 하고, 1,000명을 표본집단이라고 합니다.
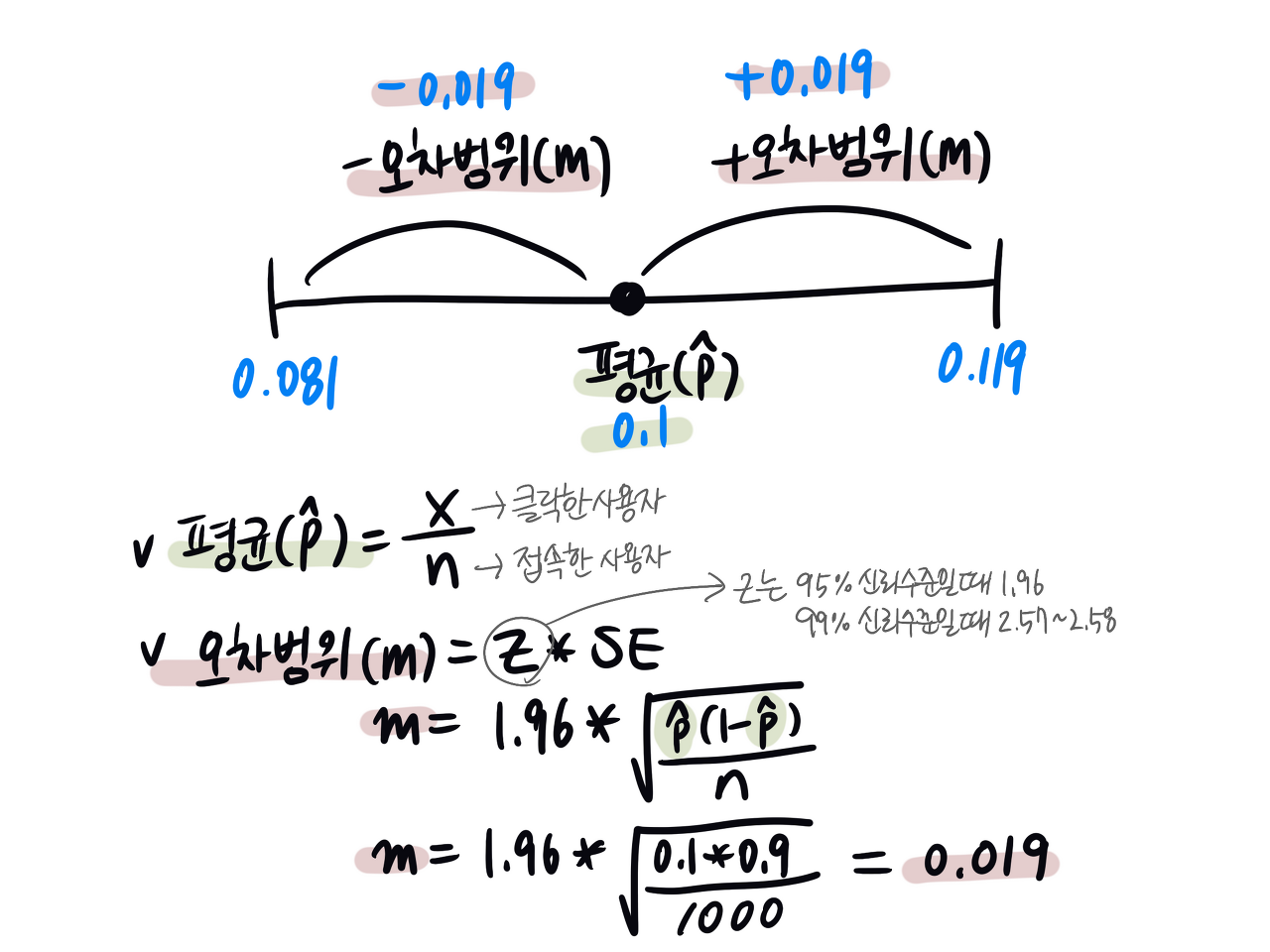
랜덤으로 뽑은 1,000명 중 100명이 버튼을 클릭했습니다. 이때 전환율은 0.1입니다. 그러나 1,000명의 전환율은 10,000명의 실제 전환율과 일치하지 않을 수 있습니다. 그래서 표본 평균을 "신뢰 구간", 즉 "표본 평균±오차 범위"의 구간으로 표시하죠. 위 예시를 95% 수준의 신뢰 구간은 "0.1±0.019"입니다. 표본집단의 전환율을 반복해서 측정하면, 전환율의 95%가 0.081~0.119 사이에서 발견되리란 뜻입니다.
신뢰 구간을 계산하는 방법은 아래와 같습니다. SE는 Standard Error (표준 오차)입니다.
2-3. 가설 검증하기
먼저 두 개의 가설을 세웁니다.
1) H0 (귀무가설): A안과 B안의 전환율 간에 차이가 없다.
2) HA (대안가설): A안과 B안의 전환율 간에 차이가 있다.
저는 귀무가설이라는 말이 어려워서 차이가 없다는 가설은 H0, 차이가 있다는 가설은 HA라고 하겠습니다.
가설 검증 시 기본적으로 H0이 사실이라고 가정합니다. 따라서 우리는 H0을 기각해야 합니다. 정리하자면, 두 조건 간 차이가 없다는 가정하에 우리가 얻은 클릭률 차이가 매우 이례적으로 발생한 값이라는 걸 검증해야 합니다. Udacity 수업의 검증 방법을 따라가 볼게요.
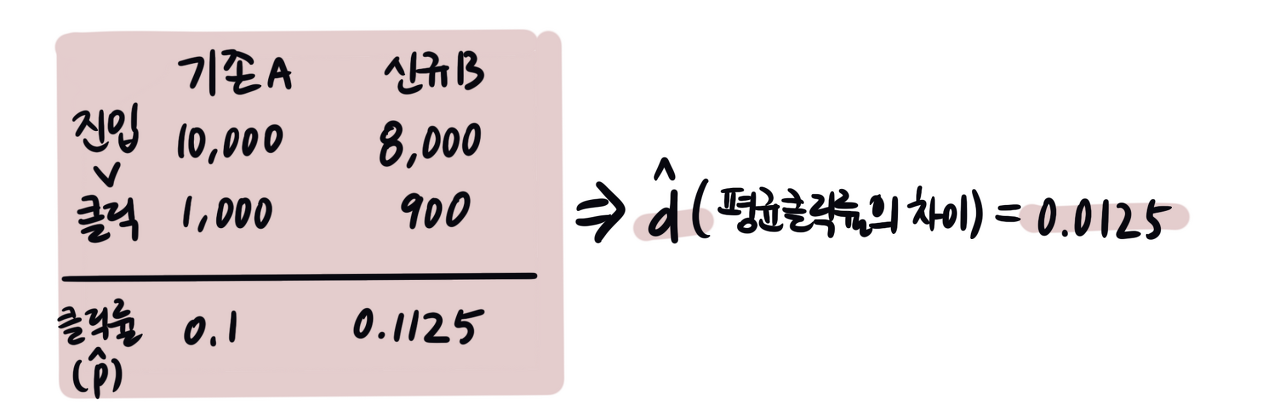
클릭률이 10%인 A안과 클릭률이 11.25%인 B안의 차이가 유의미한지 검증해볼까요? 두 조건의 클릭률의 차이는 1.25%입니다.
두 클릭률 간에 차이 없다는 H0의 그래프와 두 클릭률 간의 차이가 1.25%만큼 있다는 H1의 그래프를 그립니다.
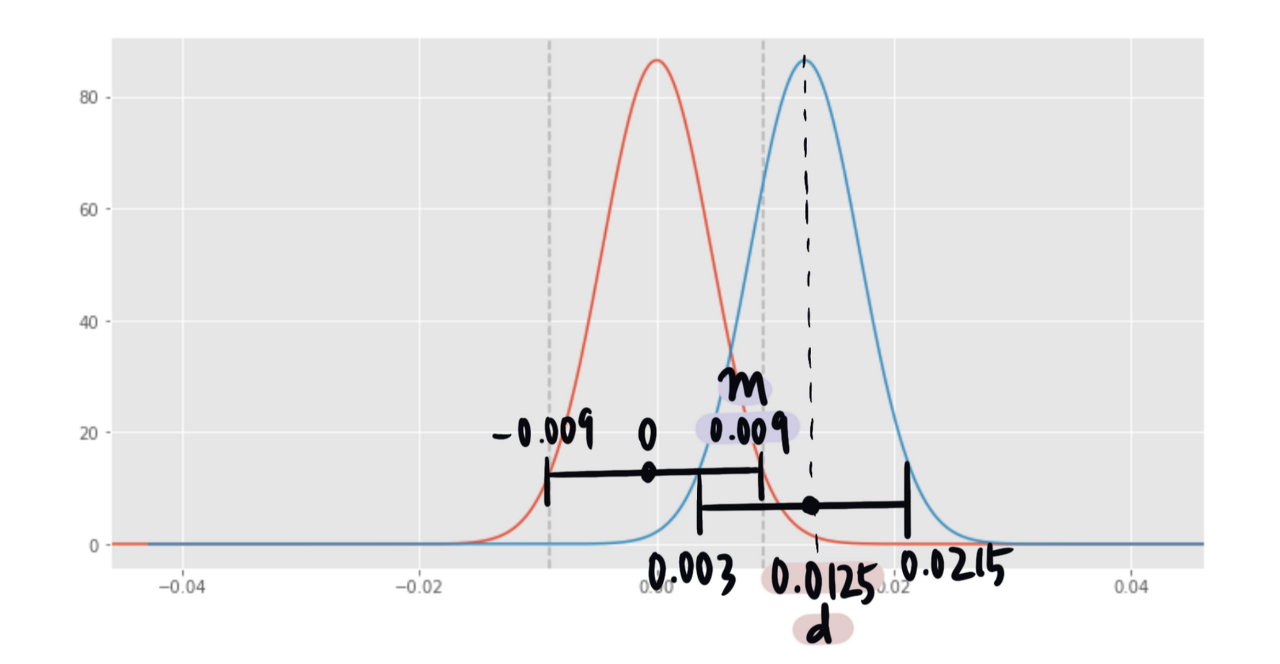
빨간색 그래프는 H0의 그래프입니다. 두 조건 간의 차이가 0인 조건의 분포이죠. 회색 점선은 H0의 신뢰 구간입니다.
파란색 그래프는 H1의 그래프입니다. H1의 중앙에 위치한 값은 A 전환율과 B 전환율의 차이입니다. 즉, 전환율 차이가 존재하는 조건의 분포입니다.
H1의 평균값(d)이 H0의 신뢰 구간 밖에 있을 때, (d<-m or d>m) H0을 기각합니다. H0이 사실이라고 했을 때 A안과 B안의 전환율 차이의 95%가 -0.009~0.009 사이에서 발견될 것입니다. H1의 평균인 0.0125는 H0의 신뢰 구간을 벗어납니다. 이 말은 H0이 사실이었을 때, 즉 두 조건 간에 차이가 없다고 했을 때, 0.0125라는 차이가 발생할 확률이 매우 낮다는 것입니다. (5% 미만) 위 그래프에서 검은색 점선이 오른쪽 회색 점선보다 우측에 위치하므로 H0을 기각하고, 통계적으로 유의하다고 결론을 내립니다.
2-4. 결과 계산하기
위의 그래프를 그리는 방법은 아래와 같습니다. 기본적으로 신뢰 구간 계산 방법과 동일합니다. 다만, 클릭률과 표준오차를 구할 때 A안과 B안의 합동 값으로 계산한다는 차이가 있습니다.
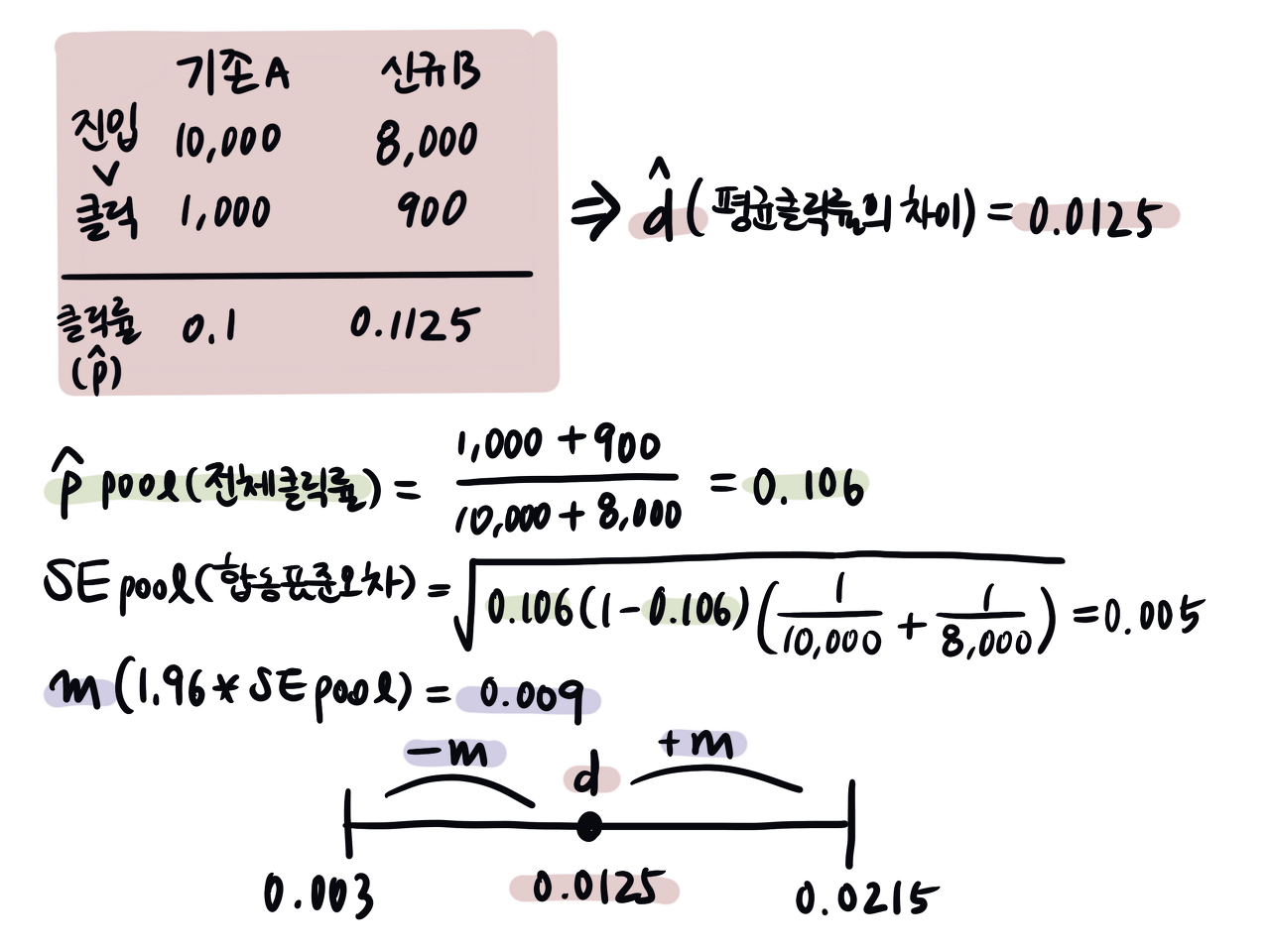
A안과 B안의 차이(d)의 신뢰 구간은 0.003~0.0215입니다. 평균 차이는 0.0125이지만, 신뢰구간을 고려해 아래와 같이 말할 수 있습니다.
A안의 전환율과 B안의 전환율의 차이가 통계적으로 유의하지만, 만약 사업 측면에서 원하는 전환율 증가가 최소 1%라면 B안은 적절하지 않습니다.
그 외 도움이 되는 정보
1) A/B 테스트 결과가 통계적으로 유의미하긴 한데, 전환율 차이가 너무 작아요. 이래도 B안을 채택할 수 있나요?
컴퓨터 공학을 전공하고 구글에서 12년간 일한 Diane Tang 박사님에 따르면, 구글에서도 1~2%만큼의 UV 전환율 차이는 꽤 크게 받아들여진다고 합니다. 실제로 Udacity 수업의 예시도 유의미한 전환율을 2%로 놓고 측정하죠. 서비스에 따라 다르겠지만, 1~3% 수준을 목표로 A/B 테스팅을 진행해도 괜찮을 것으로 보입니다.
2) A/B 테스트 계산기의 그래프는 왜 정규 분포인가요?
인터넷에 있는 A/B 테스트 계산기를 사용할 때 궁금했던 것이 있습니다. 방문자 수와 클릭한 사람의 수만 넣었는데 어떻게 정규 분포를 따를 것으로 예상했는지 알고 싶었습니다.(만약 실제로는 정규 분포가 아니라면 큰일이니까!) 데이터를 일일이 넣지 않아도 정규 분포를 예상할 수 있었던 이유는 UV 전환율 측정 방식이 이항 분포이기 때문입니다.
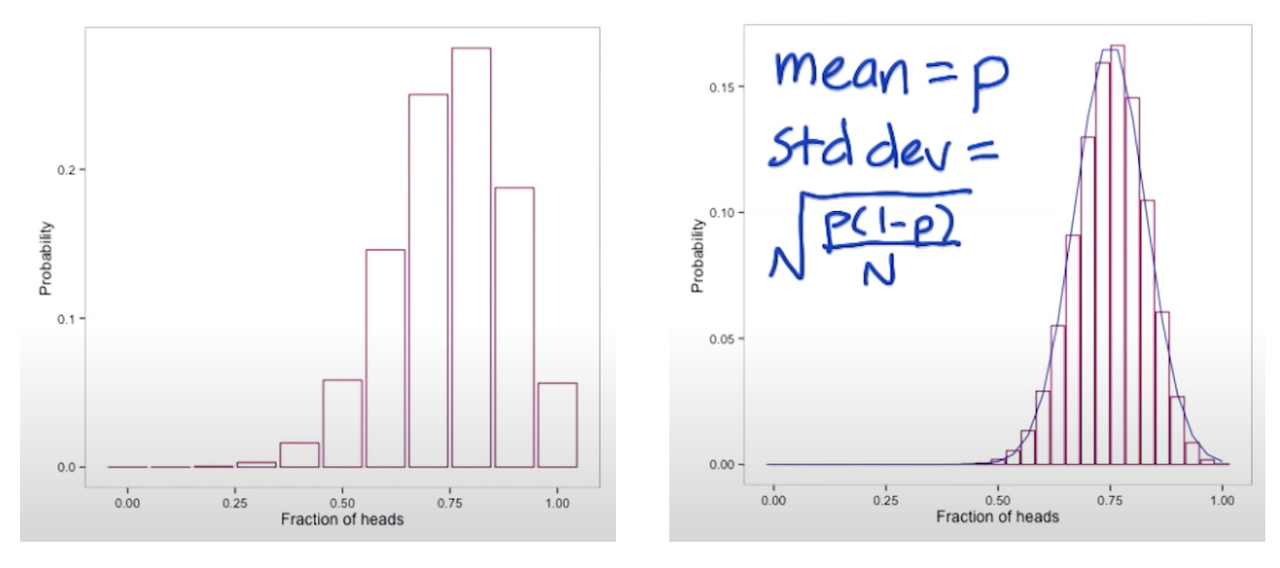
이항 분포는 N값이 높을 때 정규 분포 형태를 따릅니다. 예를 들어, 앞면이 나올 확률이 3/4인 동전이 있다고 할게요. 이 동전을 10회 던지는 시도를 여러 번 반복하고, 각 시도에 앞면이 나온 건수(비율)를 기록합니다.
그래프는 7~8회에 몰린 형태로 그려집니다. 비율로 따지면 75%에 몰린 형태입니다. 시행 횟수가 늘어날수록 그래프는 종 모양의 정규분포 형태에 가까워집니다.
*참고: 시행 횟수에 따른 분포 모양 변화를 시각적으로 잘 표현한 사이트
이 글이 A/B 테스트에 고뇌하는 분들께 도움이 되었길 바랍니다. 설명이 부족했다면 아래의 <참고 자료> 링크에서 더 많은 정보를 얻을 수 있을 거예요. 특히, Udacity A/B testing 강의를 추천합니다. 그럼 앞으로의 분석 업무에 건투를 빕니다. 화이팅!
<참고 자료>
ㆍ The Math Behind A/B Testing with Example Python Code
ㆍ p값? 신뢰구간? AB 테스트를 완성하는 통계 분석, 기본 개념 잡기
©️요즘IT의 모든 콘텐츠는 저작권법의 보호를 받는 바, 무단 전재와 복사, 배포 등을 금합니다.
