탐욕 알고리즘과 허프만 코딩 구현 방법

탐욕 알고리즘(Greedy Algorithm)은 각 단계에서 최적의 해결책을 선택하여 복잡한 문제를 간단하고 빠르게 해결하는 알고리즘을 말합니다. 이번 글에서는 탐욕 알고리즘의 기본 개념과 작동 원리를 알아보고, 알고리즘의 한계점과 적합한 문제 유형을 살펴보고자 합니다. 더불어 데이터 압축 시 사용하는 허프만 코딩(Huffman Coding)의 개념과 탐욕 알고리즘을 적용해 허프만 코딩이 어떻게 구현되는지도 함께 알아보겠습니다. 

탐욕 알고리즘이란?

1) 기본 개념 및 특징

탐욕 알고리즘은 당장 앞에 놓여 있는 선택지 중 가장 최적인 해를 선택하는 알고리즘을 말합니다. 이 알고리즘은 다양한 최적화 문제를 해결하는 데 사용되며, 각 단계에서 가장 좋아 보이는 선택을 추구하기 때문에 탐욕 알고리즘이라는 이름으로 불리고 있습니다. 

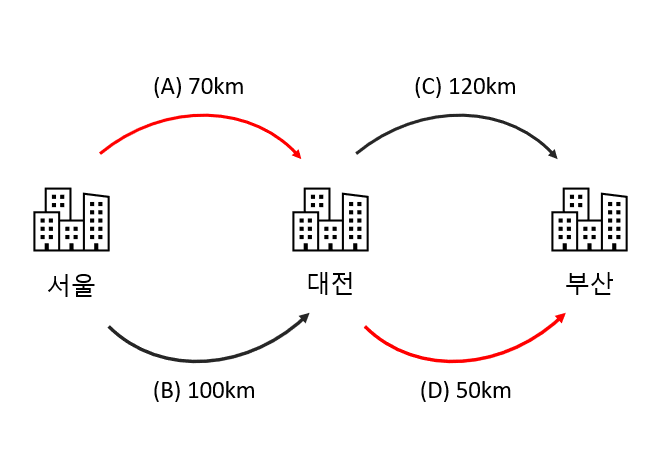
위 그림은 서울에서 대전을 거쳐 부산까지 가는 각 도로의 길이를 나타낸 그림입니다. 탐욕 알고리즘으로 서울에서 부산까지 가는 최단 루트를 찾는 경우, 먼저 서울에서 대전까지 가는 도로 중 가장 짧은 도로인 (A)를 선택합니다.

다음으로 대전에서 부산으로 가는 도로 중 가장 짧은 도로인 (D)를 선택하여, 최종적으로 (A)-(D) 루트를 선택하게 됩니다. 이처럼 탐욕 알고리즘은 각 단계에서의 최적의 선택이 전체적인 최적 해로 이어진다는 가정하에 적용된다는 특징이 있습니다.

2) 작동 원리와 장단점

앞서 살펴봤듯이 탐욕 알고리즘은 전체 문제를 부분으로 쪼개고, 각 부분에서 가장 최선인 선택을 함으로써 전체적인 문제를 해결합니다. 즉, 당장 앞에 주어진부분적인 상황만 고려하며, 전반적인 상황은 전혀 고려하지 않습니다. 따라서 탐욕 알고리즘은 복잡한 문제를 간단하고 빠르게 풀 수 있지만, 모든 문제에 대해 최적의 해를 보장하지는 않습니다.

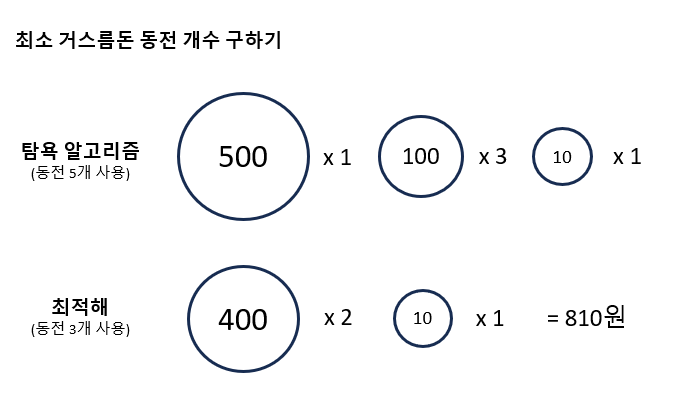
만약 위와 같이 동전 종류로 500원, 400원, 100원, 10원짜리가 있다고 가정할 때, 최소의 동전을 사용하여 거스름돈을 지불하는 문제를 풀어보겠습니다. 이 문제에 탐욕 알고리즘을 적용하면 먼저 가장 단위가 큰 500원짜리를 고려하고, 다음으로 400원, 100원, 10원짜리 동전을 고려하게 됩니다. 이에 따라 810원을 거슬러 주는 경우 500원 1개, 100원 3개, 10원 1개로 총 5개의 동전을 사용하게 됩니다.

하지만 이 문제의 최적 해는 400원짜리 2개와 10원짜리 1개를 사용하는 것입니다. 이처럼 탐욕 알고리즘은 다른 복잡한 알고리즘에 비해 간단하고 빠르지만, 400원짜리 동전이 존재하는 경우와 같은 상황에서는 항상 최적 해를 보장하지 못한다는 단점이 있습니다.

탐욕 알고리즘 조건과 적용 방법

1) 탐욕 알고리즘 조건

탐욕 알고리즘은 모든 문제에 대해 항상 최적 해를 보장하지 않지만, 다음 2가지 조건을 충족하면 최적 해를 보장할 수 있습니다.

탐욕적 선택 속성(Greedy Choice Property)

탐욕적 선택 속성이란 ‘각 단계의 선택이 이후 선택에 영향을 주지 않는다’라는 것을 말합니다. 예를 들어, 서울에서 부산으로 가는 최단 경로를 구하는 문제에서 서울에서 대전까지 가는 경로를 선택하는 것이 대전에서 부산까지 가는 경로를 선택하는 것에 어떠한 영향도 미치지 않습니다. 이러한 속성을 가진 문제는 탐욕적 선택을 계속하여 결국 최종적으로 최적 해를 구할 수 있습니다.

최적 부분 구조(Optimal Substructure)

최적 부분 구조란 ‘문제의 최종 해결책이 부분 문제의 최적 해로 구성될 수 있어야 한다’라는 것을 말합니다. 예를 들면, 서울에서 부산까지 가는 최단 경로는 서울에서 대전으로 가는 최단 경로와 대전에서 부산으로 가는 최단 경로의 합으로 구성된다는 것을 들 수 있습니다. 이러한 조건을 가지고 있는 문제는 탐욕 알고리즘을 적용하여 최적 해를 도출할 수 있습니다.

2) 탐욕 알고리즘 적용 방법

어떤 문제에 탐욕 알고리즘을 적용하려면 우선 해당 문제를 여러 부분으로 쪼개야 합니다. 그리고 앞서 살펴본 두 가지 조건인 탐욕적 선택 속성과 최적 부분 구조 조건을 충족하는지 살펴봐야 합니다. 즉, 각 단계의 선택이 다음 단계의 선택에 영향을 주는지, 각 부분의 최적 해가 최종적으로 전체 최적 해를 구성하게 되는지를 확인해야 합니다.

참고로 탐욕 알고리즘은 알고리즘 구현이 쉽고 빠르기 때문에, 위 2가지 조건을 만족하지 않더라도 다양한 문제에 활용할 수 있습니다. 특히 반드시 최적 해를 구하지 못하더라도, 어림짐작해서 답을 구해야 하는 경우에도 사용됩니다. 예를 들어, 인공지능에 활용되는 알고리즘 중 휴리스틱 탐색(Heuristic Search)이나 빔 탐색(Beam Search), A* 알고리즘 등에서 탐욕 알고리즘이 적용되고 있습니다.

허프만 코딩과 탐욕 알고리즘

1) 허프만 코딩(Huffman Coding)란?

허프만 코딩은 데이터를 효율적으로 압축하기 위한 방법을 말합니다. 여기서 데이터를 효율적으로 압축한다는 것은 텍스트, 오디오, 비디오 파일 등을 이진 코드(Binary Code)로 변환할 때 기존 방식보다 더 적은 메모리를 사용한다는 것을 의미합니다.

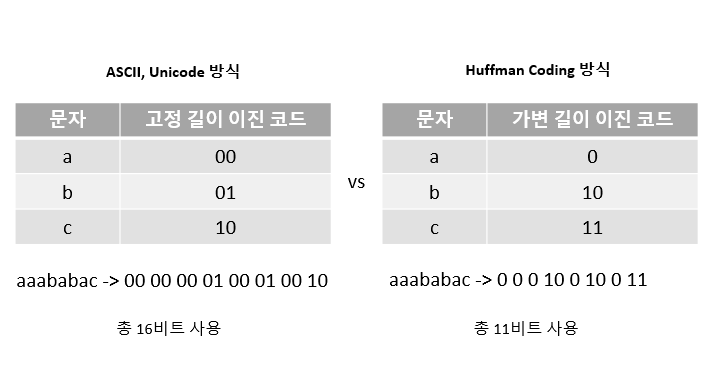
예를 들어, 위 그림과 같이 문자 종류로 a, b, c가 있고, 주어진 문자열이 aaababac인 경우를 살펴보도록 하죠. 먼저 아스키(ASCII)나 유니코드(Unicode) 같은 기존 방식은 텍스트를 이진 코드로 변환할 때 각 문자에 대해 고정된 길이의 이진 코드(Fixed-length Binary Code)를 부여합니다. 위 예시에서는 a, b, c 모두 2비트의 코드가 부여되었습니다.

반면, 허프만 코딩에서는 문자의 출현 빈도수에 따라 가변 길이 코드(Variable-length Binary Code)를 부여합니다. 위 예시에서는 출현 빈도수가 가장 많은 a는 1비트 코드로, 나머지는 2비트 코드가 부여되었습니다. 이를 통해 허프만 코딩에서는 기존 방식보다 더 적은 메모리로 데이터를 변환할 수 있는 것이죠.

2) 탐욕 알고리즘의 적용

앞서 살펴봤듯이 허프만 코딩에서는 문자열 중 자주 등장하는 문자는 짧은 비트로 표현하고, 상대적으로 자주 등장하지 않는 문자는 긴 비트로 표현합니다. 즉, 각 문자의 출현 빈도수를 기반으로 탐욕 알고리즘을 적용한 것입니다.

허프만 코딩 구현 방법

1) 전치 코드와 이진 트리 표현

허프만 코딩은 가장 적은 비트를 사용하여 문자열을 이진 코드로 변환하는 일종의 최적화 문제입니다. 따라서 허프만 코딩으로 항상 최적의 해를 구하기 위해서는 앞서 살펴본 탐욕 알고리즘의 2가지 조건을 만족해야 합니다.

첫 번째 조건인 탐욕 선택 속성은 앞선 선택이 다음 선택에 영향을 미치지 않아야 한다는 것입니다. 허프만 코딩에서는 이를 전치 코드(prefix code)라는 개념을 통해 충족시키고 있습니다. 전치 코드란 ‘한 문자의 코드가 다른 문자 코드의 앞부분이 될 수 없다’라는 규칙을 가진 코드를 말합니다. 이를 통해 이전의 코드 선택이 다음 코드 선택에 영향을 미치지 않게 됩니다.

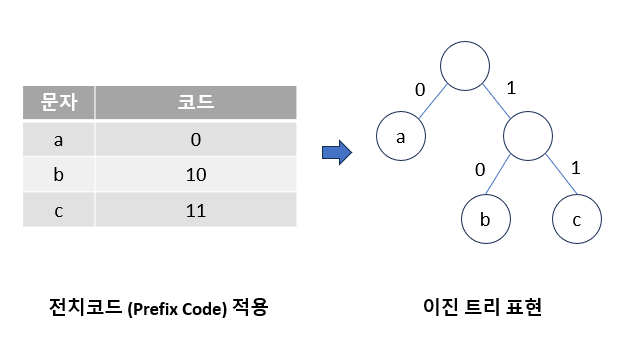
예를 들어, a의 코드가 0이라면 b나 c의 코드 앞에는 0이 올 수 없습니다. 이어서 b의 코드가 10이라면 c 코드 앞에는 10이 올 수 없는 것이죠. 이러한 전치 코드 조건은 위와 같은 이진 트리로 간단히 표현할 수도 있습니다.

2) 최적 부분 구조와 최적 해 구하기

다음으로 두 번째 조건인 최적 부분 구조에 관해 살펴보겠습니다. 최적 부분 구조는 어떤 문제의 전체적인 최적 해가 부분 문제의 최적 해의 합이라는 것을 의미합니다. 허프만 코딩에서는 전체 문제의 최적 해를 다음과 같이 각 문자의 출현 빈도수와 코드 길이를 곱한 값의 총합으로 구할 수 있습니다.

전체 문자열 코드 길이 = (각 문자의 출현 빈도수 x 각 문자의 코드 길이)의 총합

위 공식이 다소 복잡해 보일 수도 있지만, 앞선 예시를 대입하면 간단하게 이해할 수 있습니다. 앞서 살펴본 예시에서 허프만 코딩을 적용한 문자열 aaababac의 전체 코드 길이는 11비트였습니다. 이는 a:(5 x 1) + b:(2 x 2) + c:(2 x 1) = 11로 계산된 것이죠.

이는 a만 있을 때의 최적 해인 5, a와 b만 있을 때의 최적 해인 9, 마지막으로 a, b, c가 있을 때의 최적 해인 11 순으로 전체적인 최적 해를 구해 나갈 수 있다는 것입니다. 즉, 허프만 코딩은 두 번째 조건인 최적 부분 구조도 만족하기 때문에 항상 최적의 해를 보장할 수 있습니다. 그리고 여기서 최적 해를 구한다는 것은 여러 가지 코드 조합 중 전체 문자열 코드 길이가 가장 최소가 되는 값을 구하는 것을 말합니다.

3) 자바 코드 구현 예시

앞서 살펴본 내용을 토대로 자바 코드를 작성해 보겠습니다. 먼저 문자의 빈도수에 따른 이진 트리를 생성하기 위해 아래와 같이 Node 클래스를 작성합니다.

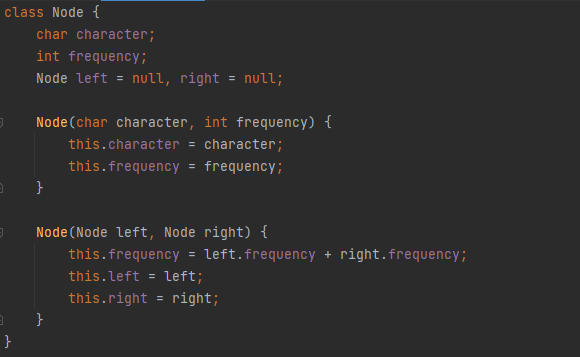
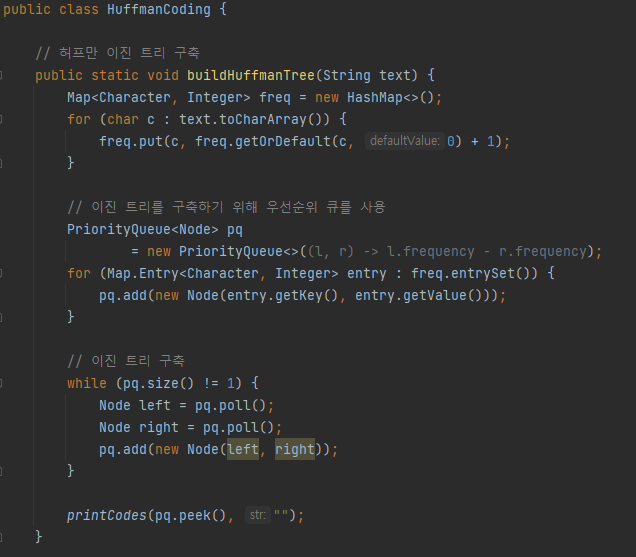
다음으로 HuffmanCoding 클래스를 만들고, 각 문자와 해당 빈도수를 가진 노드를 우선순위 큐(Priority Queue)에 추가합니다. 그리고 우선순위 큐에서 두 노드를 꺼내어 결합하고, 이를 다시 큐에 추가하는 과정을 반복하여 이진 트리를 구축합니다.

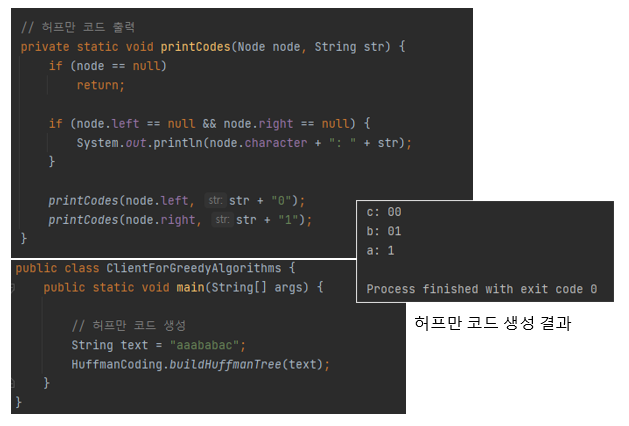
최종적으로 생성된 이진 트리를 통해 각 문자에 대한 허프만 코드를 부여하고, printCodes 메서드를 통해 각 코드를 출력합니다. 그러면 아래와 같이 aaababac 문자열에 대해 a: 1, b: 01, c:00으로 최적 이진 코드가 부여된 것을 볼 수 있습니다. 참고로, 이 결과는 0과 1만 바꿔서 a: 0, b: 10, c: 11과 동일한 결과이기도 합니다.

마치며

지금까지 탐욕 알고리즘의 기본 개념과 작동 원리, 그리고 허프만 코딩과의 관계를 살펴보고 간단하게 자바 코드로 구현해 보았습니다. 앞서 살펴본 바와 같이 탐욕 알고리즘은 탐욕 선택 속성과 최적 부분 구조 조건을 만족하는 경우 최적화 문제를 효율적으로 해결할 수 있는 알고리즘입니다. 

또한 허프만 코딩 외에도 여러 가지 실용적인 알고리즘에 사용되고 있는데요. 특히 인공지능 및 머신러닝과 관련된 다양한 최적화 문제와 의사 결정 프로세스, 그리고 복잡한 데이터 패턴의 해석과 같은 문제에도 활용되고 있으니, 미리 학습해 두는 것을 추천합니다.

©️요즘IT의 모든 콘텐츠는 저작권법의 보호를 받는 바, 무단 전재와 복사, 배포 등을 금합니다.