자료구조 개념 이해하기 ‘힙과 힙 정렬 알고리즘’

자료구조란 데이터를 효율적으로 저장, 검색, 삭제할 수 있도록 설계된 구조나 방법을 의미합니다. 이 중에서 힙(Heap)은 정렬, 우선순위 큐, 스케줄링과 같은 다양한 알고리즘에서 활용되는 자료구조입니다. 이번 글에서는 힙에 대한 기본적인 개념과 구현 방법을 소개하고, 힙을 활용한 정렬 알고리즘에 대해 살펴볼까 합니다. 더불어 힙 정렬의 시간 복잡도를 분석하여 어떤 경우에서 힙을 사용하는 것이 적절한지에 대해서도 알아보겠습니다.

힙(Heap) 개념 살펴보기

1) 힙의 정의

힙은 완전 이진 트리(Complete Binary Tree)의 일종으로, 부모 노드와 자식 노드 간에 특정한 조건을 만족하는 자료구조를 말합니다. 여기서 완전 이진 트리란 부모 노드 밑에 자식 노드가 최대 2개까지 있을 수 있고, 마지막 레벨을 제외한 모든 레벨에 노드가 완전히 채워져 있는 트리 구조를 말합니다.

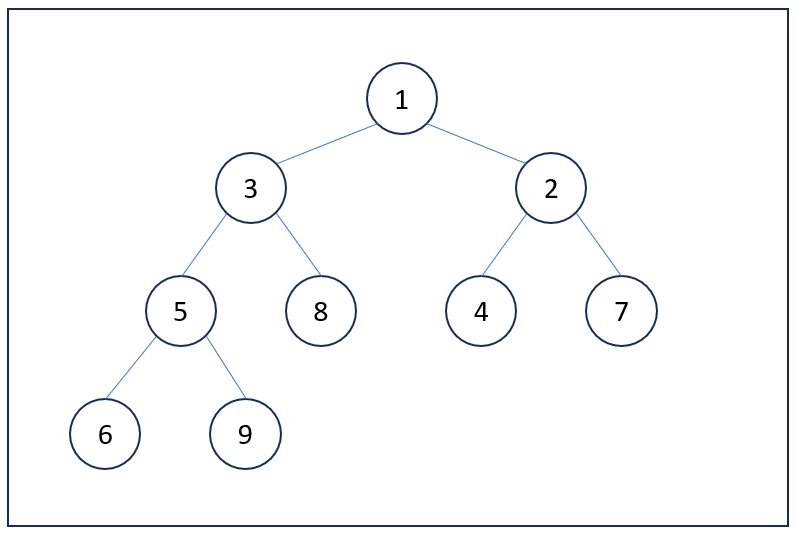
힙에서는 부모 노드, 자식 노드, 루트, 리프, 레벨, 높이와 같은 용어들이 사용됩니다. 힙을 이해하기 위해서는 먼저 이러한 기본적인 용어들을 알아두어야 합니다. 각 용어에 대한 설명은 다음과 같습니다.

1. 부모 노드(Parent Node), 자식 노드(Child Node): 특정 노드의 상위에 위치한 노드를 부모 노드라고 하며, 특정 노드의 하위에 위치한 노드를 자식 노드라고 합니다.

2. 루트 노드(Root Node), 리프 노드(Leaf Node): 트리 구조에서 가장 상위에 위치한 노드를 루트 노드라고 합니다. 반면, 가장 밑에 위치하면서 자식 노드가 없는 노드를 리프 노드라고 합니다.

3. 레벨(Level), 높이(Height): 레벨은 루트 노드부터 시작하여 트리의 몇 번째 층에 있는지를 나타냅니다. 보통 루트 노드의 레벨은 0으로 표시합니다. 레벨과 달리 트리의 높이는 리프 노드부터 시작하며, 루트 노드의 높이는 트리의 전체 높이가 됩니다.

2) 힙의 종류

힙의 종류에는 최대 힙(Max-Heap)과 최소 힙(Min-Heap)이 있습니다. 최대 힙은 모든 부모 노드가 그 자식 노드보다 크거나 같은 값을 갖는 특성을 가집니다. 이러한 특성 때문에 루트 노드는 전체 힙 중에서 가장 큰 값을 가집니다. 다음 그림은 최대 힙의 예시입니다.

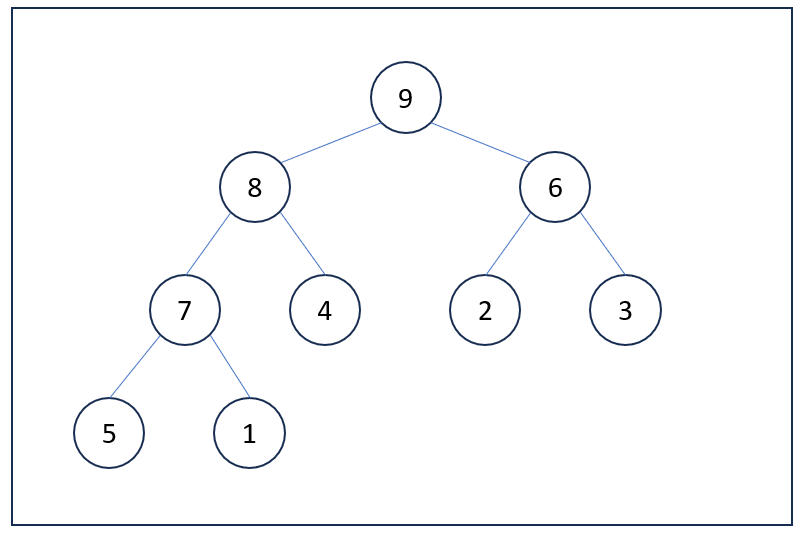
반대로 최소 힙은 모든 부모 노드가 자식 노드보다 작거나 같습니다. 그리고 트리의 루트 노드는 전체 힙 중에서 가장 작은 값을 가집니다. 앞서 힙의 정의에서 살펴본 완전 이진 트리가 바로 최소 힙의 예입니다.

힙 구현 예시 살펴보기

1) 힙 구현 방법

힙은 보통 배열(Array)을 이용해서 구현합니다. 아래 그림과 같이 루트 노드(9)는 배열의 첫 번째 인덱스에 위치하게 됩니다. 인덱스가 1부터 시작하는 배열의 경우, i 인덱스에 있는 노드의 왼쪽 자식 노드는 2 x i 인덱스에 위치하며, 오른쪽 자식 노드는 2 x i + 1 인덱스에 위치합니다.

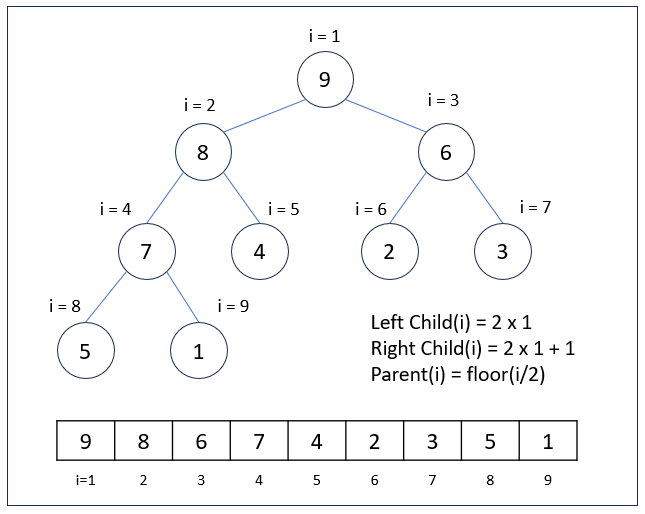
예를 들어, 루트 노드(9)의 인덱스는 1이기 때문에 왼쪽 자식 노드(8)의 인덱스는 2 x 1 = 2가 되고, 오른쪽 자식 노드(6)의 인덱스는 2 x 1 + 1 = 3이 됩니다.

2) 힙 구현 코드 예시

이제 자바 코드로 힙을 구현해 보겠습니다. 아래 코드는 최소 힙을 구현한 예시 코드입니다. 먼저 주어진 배열을 복사하고, 편의상 루트 노드가 인덱스 1부터 시작하도록 합니다. 참고로, build_heap() 메서드 이름은 최소 힙을 구축하는 예시이기 때문에 build_min_heap()으로 했습니다.

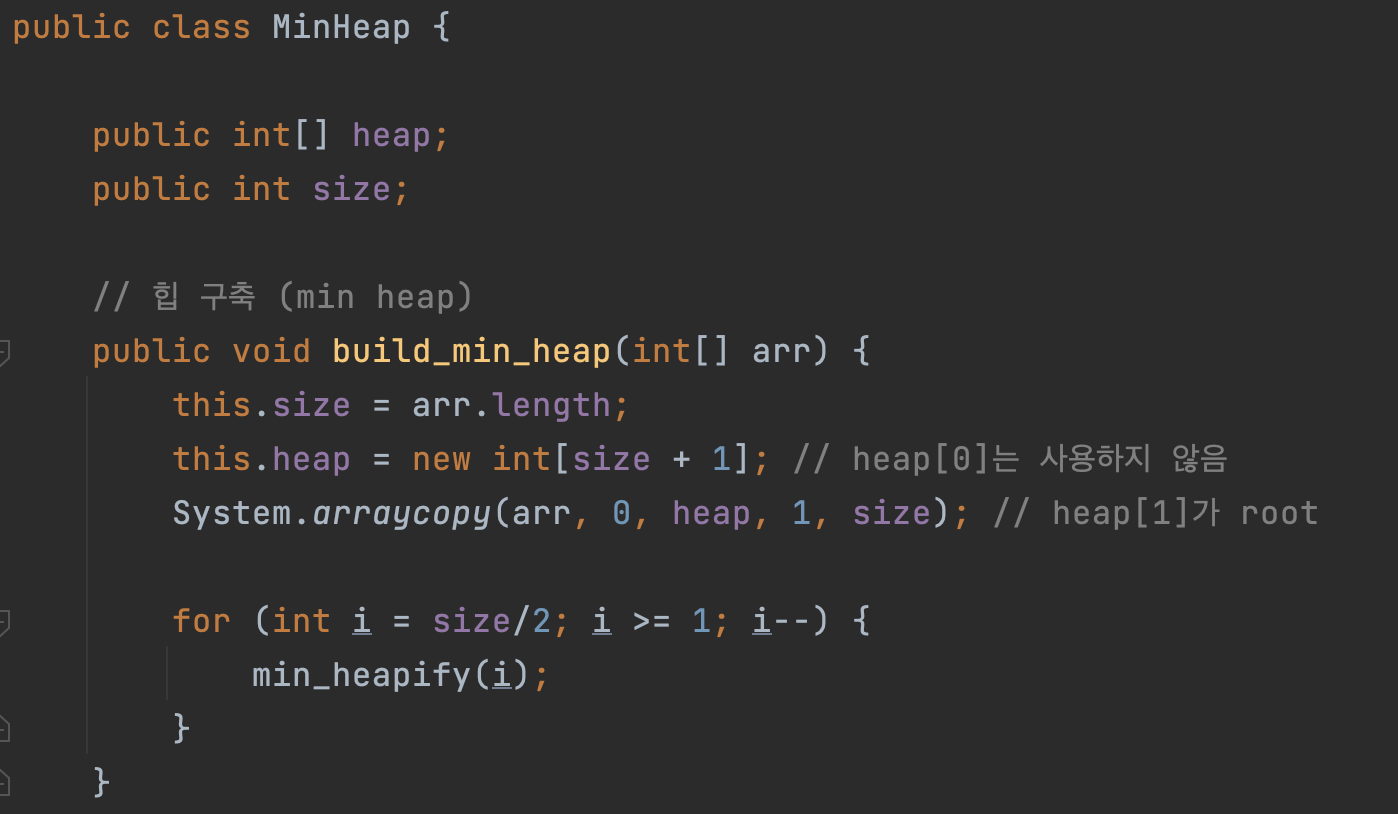
다음으로 heapify()라는 메서드를 호출합니다. 여기서도 heapify() 메서드 이름은 최소 힙 예시이기 때문에 min_heapify()라고 붙였습니다. heapify()는 힙의 조건에 맞게 노드의 위치를 재배열하는 역할을 합니다.

이제 build_min_heap()의 for문에서 부모  노드들을 역으로 순회하면서  heapify() 메서드를 호출하여 힙을 구성합니다. 여기서 힙의 가장 마지막에 위치한 부모 노드의 인덱스는 전체 힙 사이즈를 2로 나눈 값입니다.

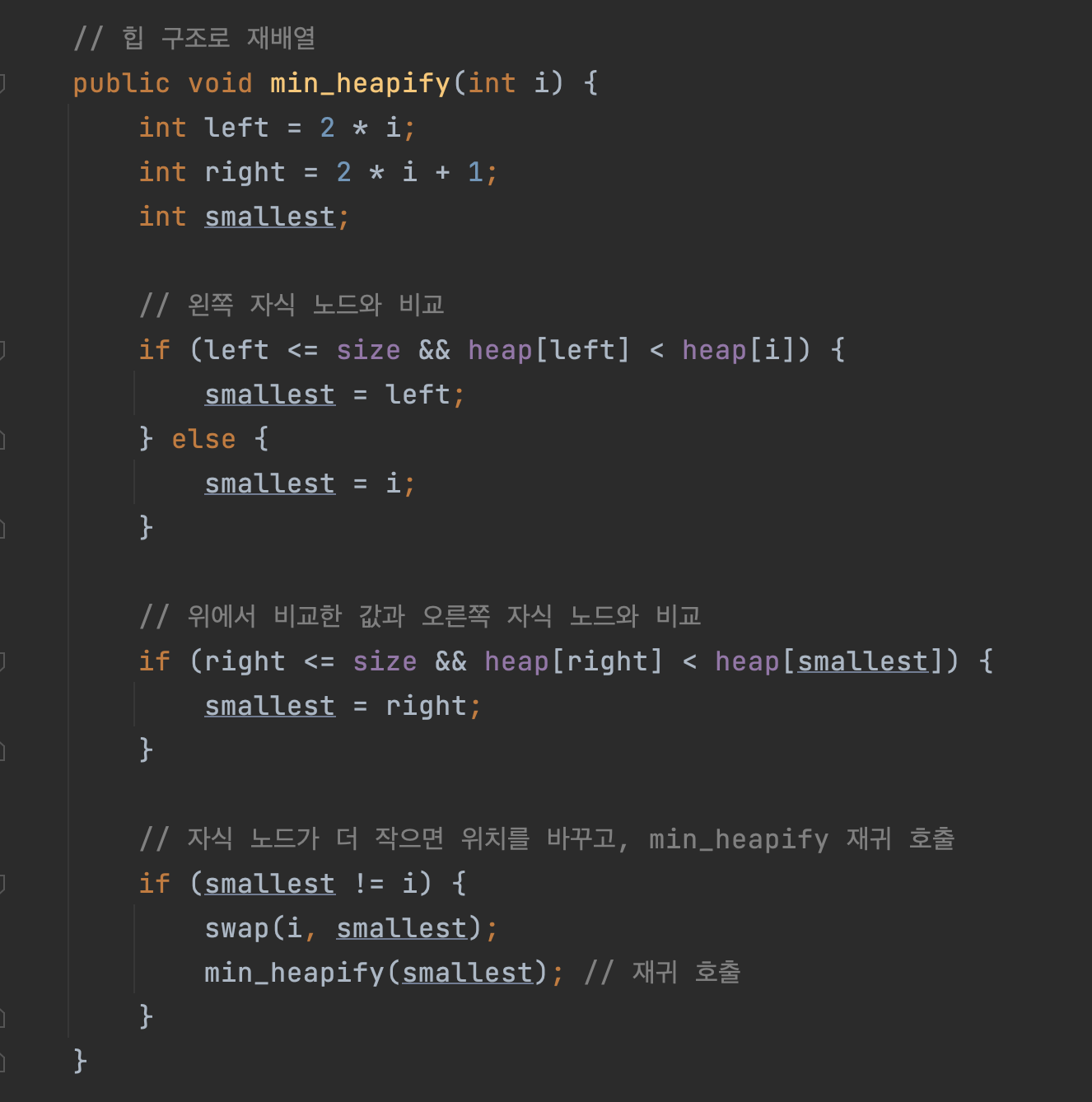
heapify()는 최소 힙에서 부모 노드가 자식 노드보다 큰 경우 위치를 바꿉니다. 그리고 이 과정을 재귀적으로 진행하여 전체 힙이 최소 힙의 조건을 만족하도록 합니다. 여기서 말하는 최소 힙의 조건이란 모든 부모 노드는 자식 노드보다 작거나 같아야 한다는 조건을 말합니다.

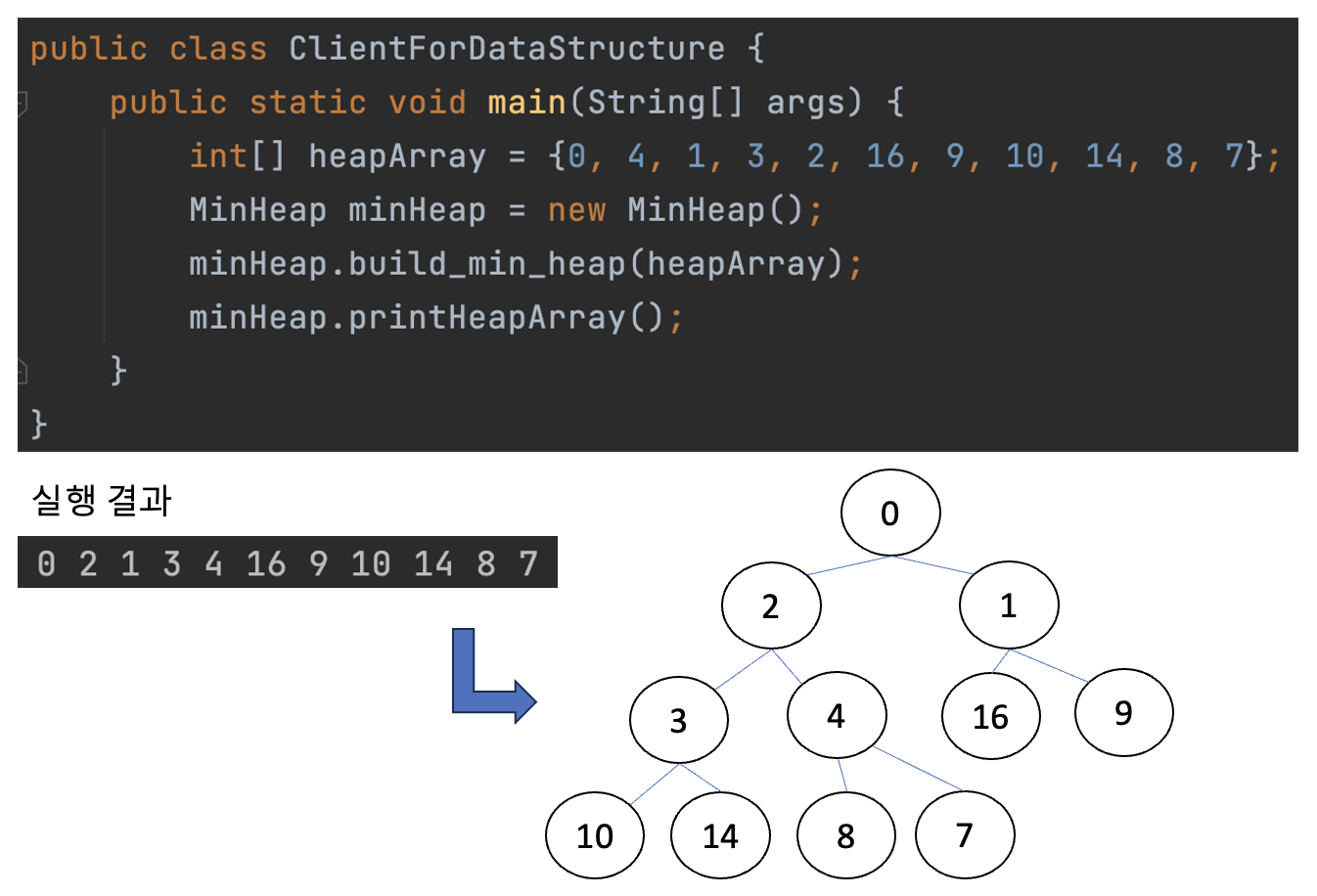
이제 구현된 힙을 클라이언트 코드에서 호출해 보겠습니다. 그러면 아래와 같이 최소 힙의 조건에 맞게 주어진 배열이 재배치됩니다. 재배치된 배열을 트리로 표현하면 최소 힙이 된다는 것을 볼 수 있습니다.

3) 힙 시간 복잡도 분석

힙을 재배열할 때 사용하는 heapify() 연산은 O(log n)의 시간 복잡도를 가집니다. 그 이유는 heapify()가 힙의 높이만큼 재귀 호출을 하기 때문인데요. 예를 들어, 자식 노드가 최대 2개인 힙에서 전체 노드의 개수가 n이고, h가 힙의 높이라면 n이 4일 때 h는 2가 되고, n이 8일 때 h는 3이 됩니다. 즉, 이를 계산 식으로 표현하면 높이 h = log2n가 됩니다. 따라서 heapify()의 시간 복잡도는 O(log n)가 됩니다.

힙을 구축하는 build_heap()은 일반적으로 O(n)의 시간복잡도를 가집니다. 아울러 힙의 삽입과 삭제 연산을 할 경우에는 노드의 삽입 또는 삭제 후 트리를 재정렬하기 때문에, 힙의 높이에 따른 O(log n) 시간 복잡도를 갖게 됩니다. 전체 힙의 최대값 또는 최소값을 구하는 경우, 단순히 힙의 루트 값을 조회하면 되기 때문에 O(1)의 시간 복잡도를 갖습니다.

힙을 이용한 정렬 알고리즘

1) 힙 정렬(Heap Sort)

힙 정렬은 힙을 이용하여 배열을 정렬하는 알고리즘입니다. 힙 정렬에서는 정렬되지 않은 배열을 최대 힙이나 최소 힙으로 구성하고, 루트 노드를 가장 마지막 노드와 교환한 후 힙 크기를 줄이는 방식으로 정렬을 수행합니다.

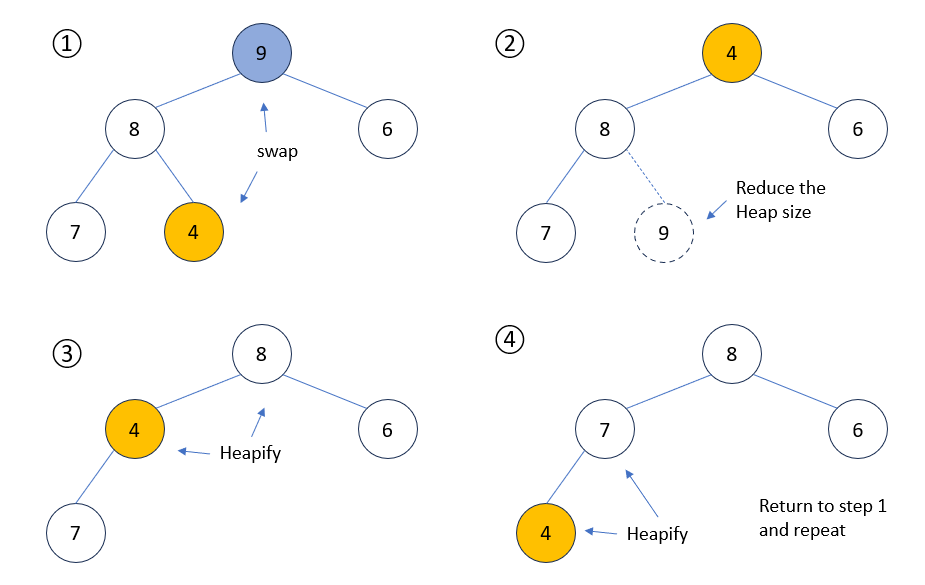
예를 들어, 위 그림처럼 최대 힙으로 구성된 [9, 8, 6, 7, 4] 배열에서 가장 마지막 요소인 [1]을 힙의 최댓값이자 루트 노드인 [9]와 교환합니다. 그리고 배열의 마지막 자리가 확정된 [9]를 제외하기 위해 힙 크기를 줄이고, heapify()를 재귀 호출하여 다시 전체 트리를 최대 힙으로 만듭니다. 이 과정을 반복하면 최종적으로 [4, 6, 7, 8, 9]로 정렬된 배열을 만들 수 있습니다.

2) 힙 정렬 구현 예제

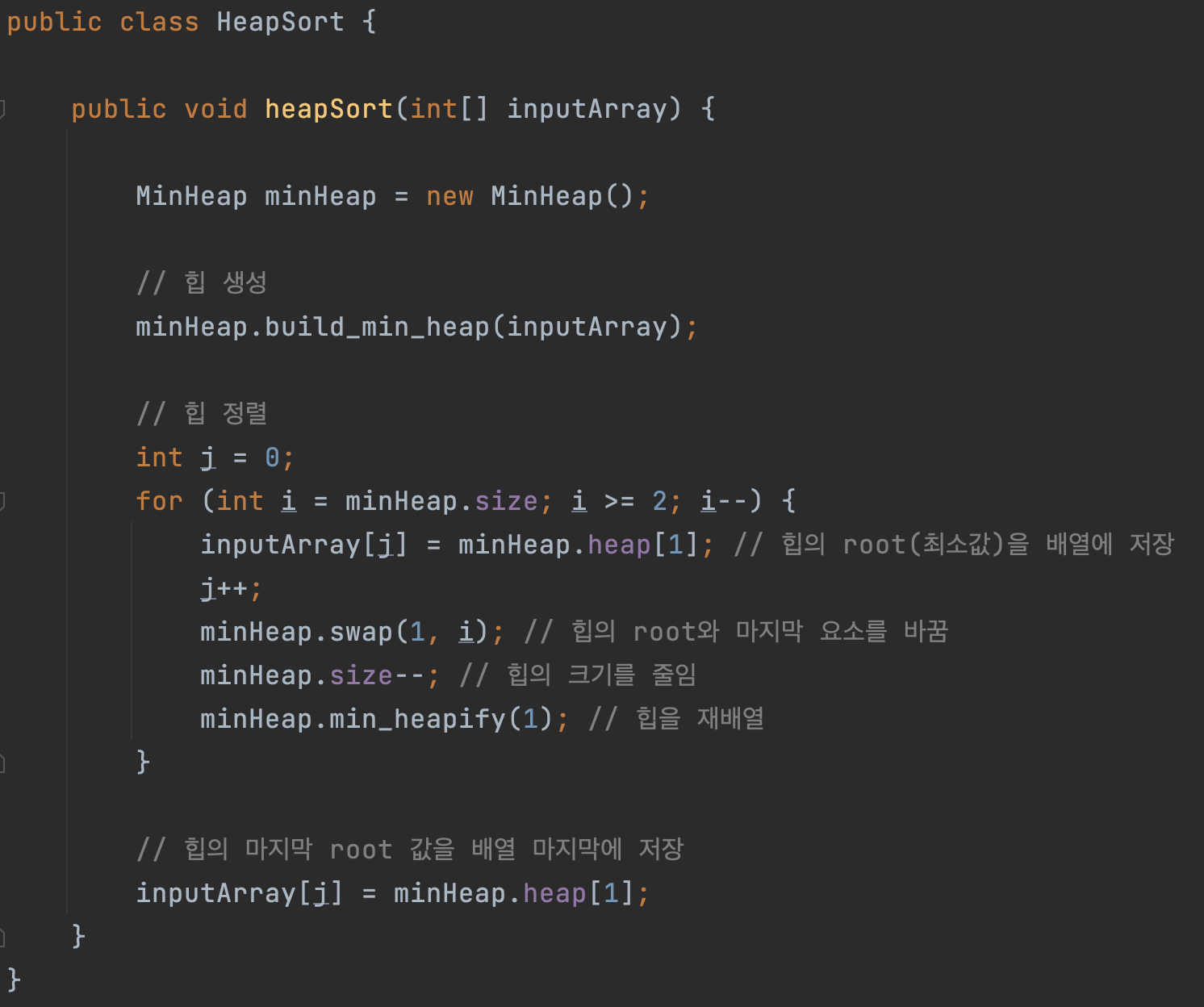
다음 예시 코드는 앞서 구현한 최소 힙을 이용하여 힙 정렬을 구현한 코드입니다. 앞서 설명한 바와 같이 루트 노드와 마지막 노드의 교환, 힙 크기 축소, 전체 힙 재배열(heapify)의 과정을 거칩니다.

힙 정렬 시간 복잡도 분석하기

1) 시간 복잡도 분석 

힙 생성은 일반적으로 O(n)의 시간 복잡도를 가집니다. 그리고 힙 정렬에서는 힙에서 가장 큰(또는 작은) 원소를 제거하고, 힙을 재정렬하는 과정을 n번 반복합니다. 각 제거 연산은 O(log n)의 시간 복잡도를 가지기 때문에 이 과정에서의 시간 복잡도는 O(n log n)가 됩니다. 따라서 힙 생성을 포함한 힙 정렬의 전체 시간 복잡도는 다음과 같은 빅오 표기법에 따라 O(n log n)입니다.

O(n) + O(n log n) = O(n log n)

2) 다른 정렬 알고리즘과의 비교

앞서 정렬 알고리즘 글에서 살펴본 다른 정렬 알고리즘과 시간 복잡도를 비교해 보면 다음 표와 같습니다. 힙 정렬은 일반적으로 사용되는 퀵 정렬, 병합 정렬과 같이 평균 O(n log n)의 시간 복잡도를 가집니다. 또한 최악, 최선의 경우에도 모두 O(n log n)의 일정한 시간 복잡도를 보입니다.

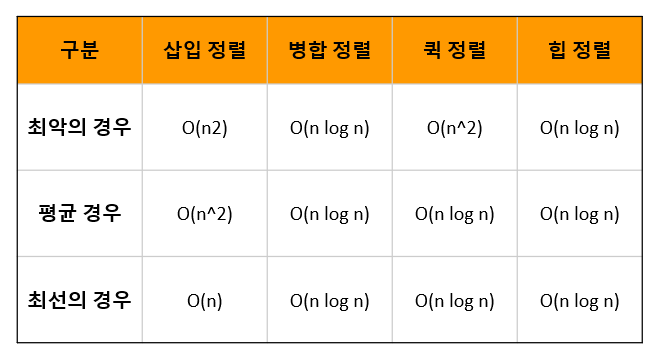
힙 정렬은 퀵 정렬과 마찬가지로 별도의 메모리를 사용하지 않는 제자리 정렬(in-place sorting) 방식을 사용합니다. 따라서 힙 정렬은 일정한 성능을 보임과 동시에 별도의 메모리를 사용하지 않는다는 장점이 있습니다.

또한 각 원소가 k 위치만큼 떨어져 있는 배열인 이른바 k-sort 배열을 정렬할 때 가장 효율적인 방법으로 사용되기도 합니다. 다만 숫자가 같은 경우에도 스왑이 일어날 수 있기 때문에, 퀵 정렬과 함께 안정적이지 않은 정렬 방법으로 분류된다는 점도 알아두는 것이 좋습니다.

마치며

지금까지 자료구조 힙과 힙을 이용한 정렬 알고리즘 힙 정렬에 대해서 살펴봤습니다. 힙과 힙 정렬은 각각 효율적인 데이터 관리 및 빠른 정렬을 가능하게 하는 자료구조와 알고리즘입니다. 특히 힙은 정렬 알고리즘을 비롯하여, 우선순위 큐, 스케줄링, 그리고 여러 검색 알고리즘에서도 중요한 역할을 하므로 꼭 공부해 두길 바랍니다.

요즘IT의 모든 콘텐츠는 저작권법의 보호를 받는 바, 무단 전재와 복사, 배포 등을 금합니다.