알아두면 유용한 정렬 알고리즘과 시간 복잡도 분석

정렬 알고리즘은 데이터베이스 시스템, 검색 엔진, 머신러닝 알고리즘, 일상생활의 다양한 디지털 서비스에서 활용됩니다. 알고리즘의 효율성은 보통 시간 복잡도(Time Complexity)로 나타내며, 프로그램 성능에 큰 영향을 미칠 수 있으므로 최적화하는 것이 중요합니다.

이번 글에서는 정렬 알고리즘의 종류 중 삽입 정렬, 병합 정렬, 퀵 정렬에 대해 살펴보고, 각 알고리즘의 시간 복잡도를 비교하여 어떤 경우에 사용해야 하는지 알아보도록 하겠습니다.

삽입 정렬 알고리즘(Insert Sort)

1) 동작 원리

삽입 정렬(Insertion Sort) 알고리즘은 배열의 각 요소를 적절한 위치에 삽입하는 방식으로 동작합니다. 초기에는 배열의 첫 번째 요소를 이미 정렬된 것으로 간주하고, 2번째 요소부터 시작합니다. 그리고 반복문으로 해당 요소와 가장 가까운 좌측 요소부터 비교하면서 삽입 위치를 확인합니다.

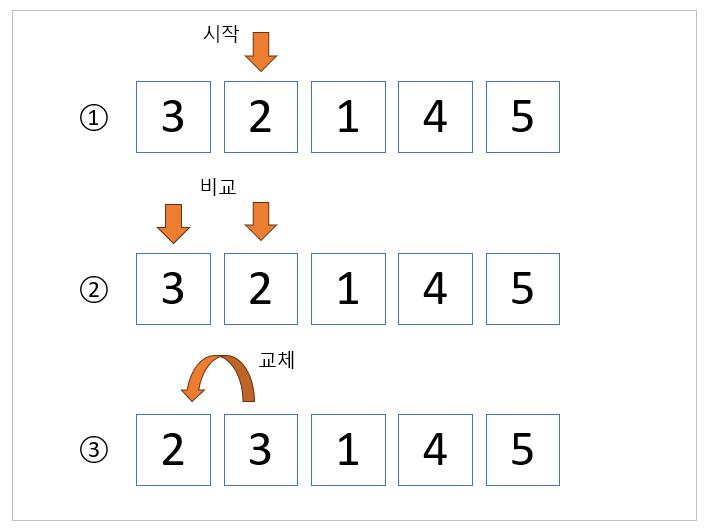
예를 들어, 위 그림과 같이 [3, 2, 1, 4, 5]이라는 배열이 있는 경우, 첫 번째 단계에서는 2번째 요소인 [2]를 먼저 선택합니다. 다음으로 [2]를 좌측에 있는 요소와 하나씩 비교합니다. 여기서는 [3] > [2]이기 때문에 두 위치를 바꿔줍니다. [2]의 좌측에는 더이상 숫자가 없기 때문에 비교를 종료합니다.

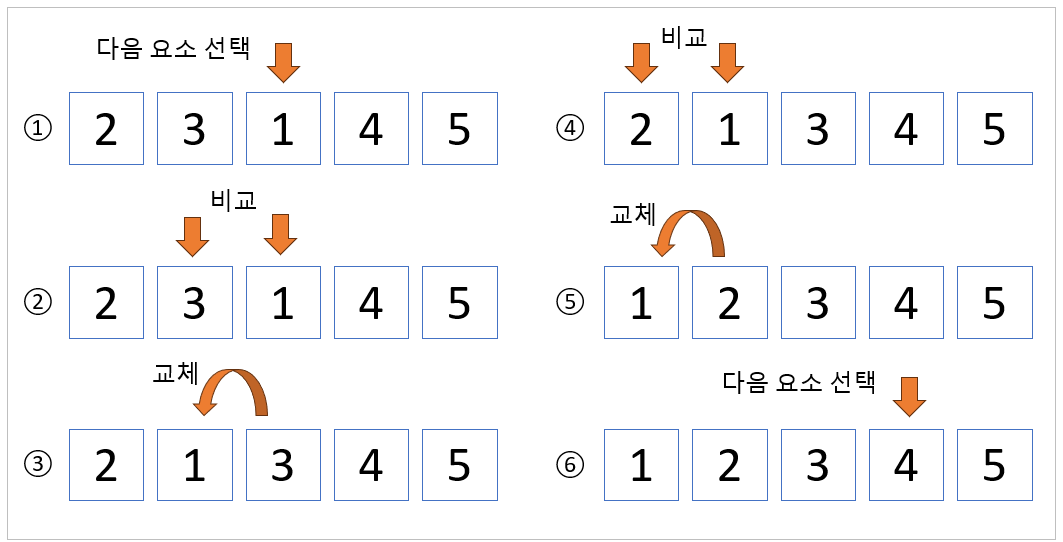
다음에는 3번째 요소인 [1]을 선택하여 좌측에 있는 숫자들과 비교합니다. 먼저 [3]과 비교해서 자리를 바꾸고 다음으로 [2] 비교해서 자리를 바꿉니다. 그리고 다음 4번째 요소인 [4]로 이동합니다. [4]부터는 좌측에 있는 숫자 중 큰 숫자가 없기 때문에 그 자리를 그대로 유지합니다. 삽입 정렬 알고리즘은 이러한 방식으로 숫자 배열을 정렬합니다.

2) 코드 예시

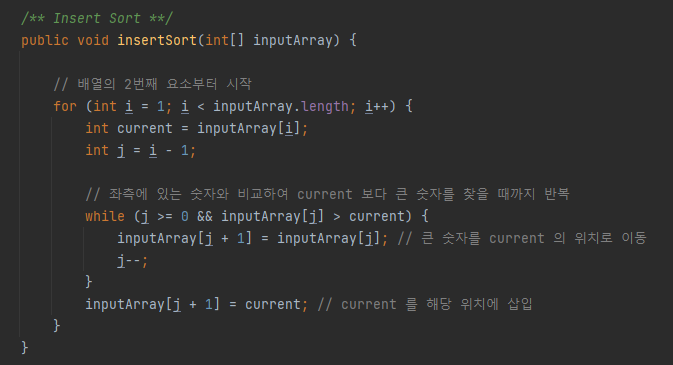
다음은 삽입 정렬 알고리즘을 구현한 자바 코드 예시입니다. for문에서는 i = 1로 설정하여 배열의  2번째 요소부터 시작합니다. 그리고 while문으로 좌측에 있는 숫자와 비교하여 큰 숫자가 있는 경우 위치를 바꿉니다.

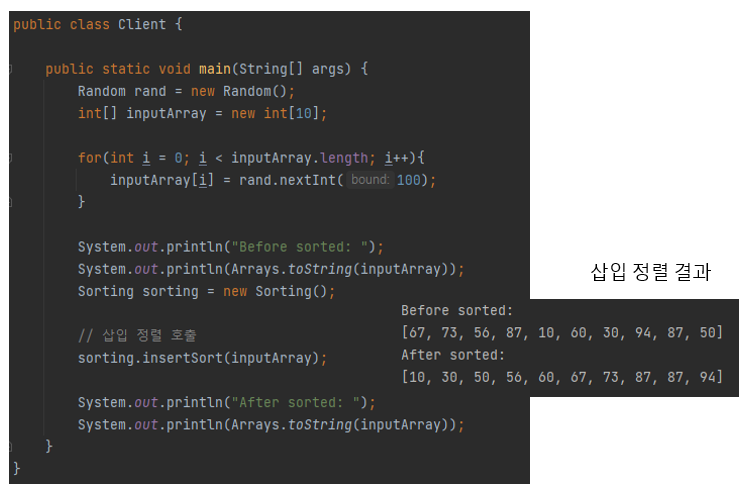
이제 클라이언트 코드에서 insertSort() 메서드를 호출하여 임의의 숫자 배열을 정렬해 보도록 하겠습니다. 코드를 실행하면 아래 그림과 같이 배열이 정렬되는 것을 확인해 볼 수 있습니다.

병합 정렬 알고리즘(Merge Sort)

1) 동작 원리

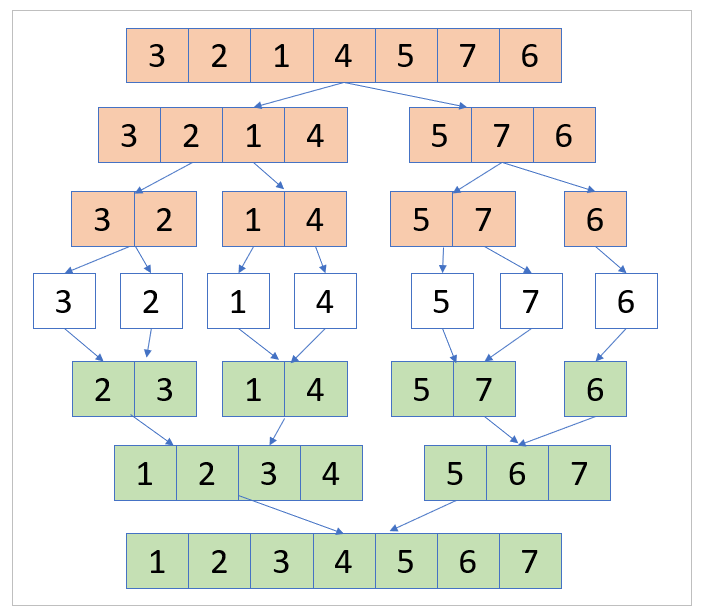
병합 정렬(Merge Sort)은 대표적인 분할 정복(Divide and Conquer) 알고리즘 중 하나입니다. 병합 정렬에서는 먼저 배열을 두 개의 부분 배열로 분할하고, 각 부분 배열을 정렬하는 분할 정복 단계를 거칩니다. 그리고 두 개의 정렬된 부분 배열을 병합하여 최종적으로 하나의 정렬된 배열을 만드는 방식으로 동작합니다.

• 분할(Divide)

주어진 배열을 두 개의 동일한 크기의 부분 배열로 분할합니다. 만약 배열의 크기가 홀수라면, 부분 배열은 다른 부분 배열보다 원소가 하나 더 많을 수 있습니다.

• 정복(Conquer)

정복 단계에서는 두 개의 부분 배열을 정렬합니다. 만약 두 배열의 크기를 다시 나눌 수 있다면, 다시 분할 단계로 재귀적 호출(recursive call)을 진행합니다.

• 병합(Merge)

두 개의 정렬된 부분 배열을 병합하여 하나의 정렬된 배열로 만듭니다. 이 과정은 두 부분 배열의 첫 번째 요소부터 비교하여 작은 숫자를 병합된 배열에 차례대로 넣는 방식으로 진행됩니다. 결과적으로 두 부분 배열의 모든 원소가 병합된 배열로 이동할 때까지 병합 단계를 반복합니다.

2) 코드 예시

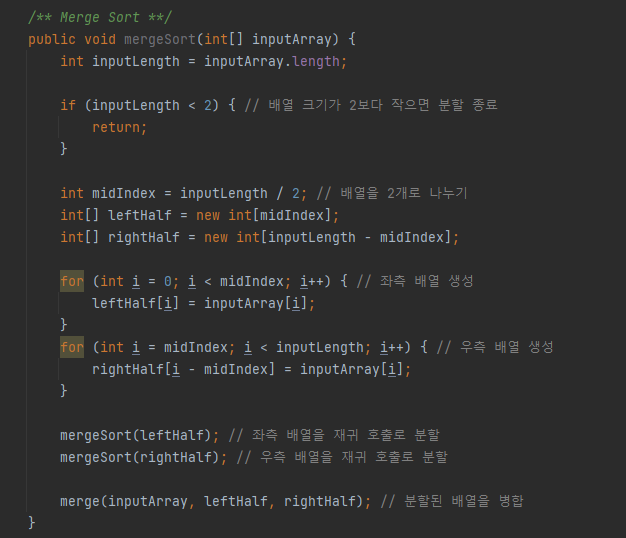
다음 코드는 병합 정렬 알고리즘을 구현한 자바 코드입니다. mergeSort() 메서드에서 먼저 배열의 크기를 체크하여, 가장 작은 단위의 배열 크기가 되면 재귀 호출에서 빠져나오도록 조건(Base Case)을 설정합니다. 그리고 기존 배열을 2개로 분할하고, 각 배열에 대한 mergeSort() 재귀 호출과 병합 메서드인 merge()를 호출하도록 합니다.

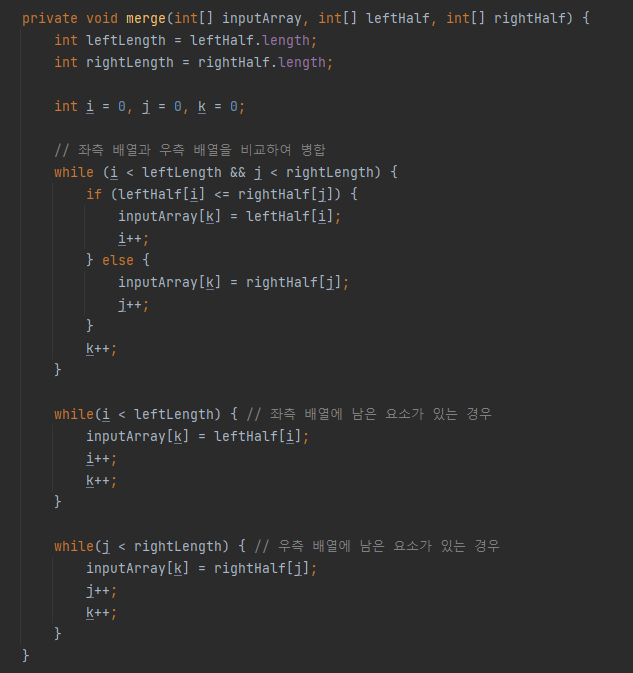
merge() 메서드에서는 두 배열의 좌측 숫자부터 비교하여 작은 숫자를 차례대로 병합된 배열에 넣습니다. 만약 한 쪽 배열의 숫자가 남아 있으면 while loop로 병합된 배열에 남은 숫자들을 채워줍니다.

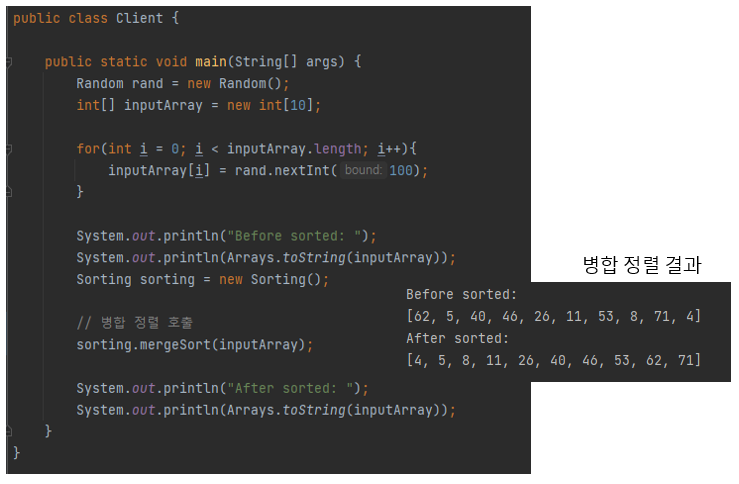
이제 앞선 삽입 정렬과 마찬가지로 클라이언트 코드에서 병합 정렬 메서드를 호출하여 결과를 확인해 보면, 다음 그림과 같이 배열이 잘 정렬되는 것을 볼 수 있습니다.

퀵 정렬 알고리즘(Quick Sort)

1) 동작 원리

퀵 정렬(Quick Sort)도 분할 정복 전략을 사용하는 정렬 알고리즘입니다. 퀵 정렬은 배열에서 피벗(Pivot)을 선택하고, 피벗을 기준으로 파티션(Partition)을 나누어 배열을 정렬하는 방식으로 진행됩니다. 병합 정렬과 다른 점은 퀵 정렬에서는 병합 과정이 필요하지 않다는 것입니다. 분할 과정에서 피벗으로 선택된 요소들이 배열 내에서 자신의 최종 위치에 배치되기 때문입니다.

• 피벗 선택(Pivot Selection)

배열에서 요소 하나를 피벗으로 선택합니다. 피벗 선택 방법은 여러 가지가 있으며, 이에 따라 알고리즘의 성능이 달라지기도 합니다.

• 분할(Partition)

선택한 피벗을 기준으로 배열을 두 개의 부분 배열로 분할합니다. 피벗보다 작거나 같은 원소들은 좌측 부분 배열에, 피벗보다 큰 원소들은 우측 부분 배열에 위치하게 됩니다.

• 정복(Conquer)

두 개의 부분 배열을 재귀적으로 호출하며, 부분 배열의 크기가 0 또는 1이 될 때까지 반복합니다.

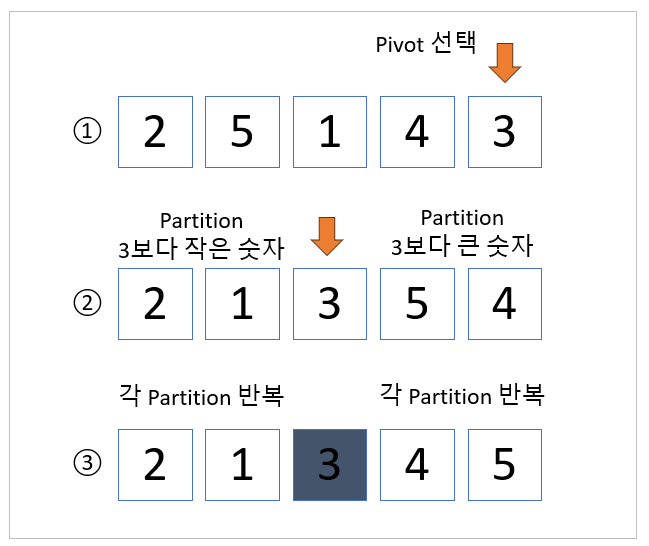
예를 들어, 위 그림처럼 [2, 5, 1, 4, 3] 배열을 퀵 정렬로 정렬하는 경우 우선 배열의 가장 마지막 요소인 [3]을 피벗으로 선택합니다. 그다음 피벗 [3]을 기준으로 [2, 1]과 [4, 5] 두 개의 파티션으로 분할합니다. 각 파티션에 대해 재귀 호출을 하여 앞선 과정을 반복하면서 전체 배열을 정렬합니다.

2) 코드 예시

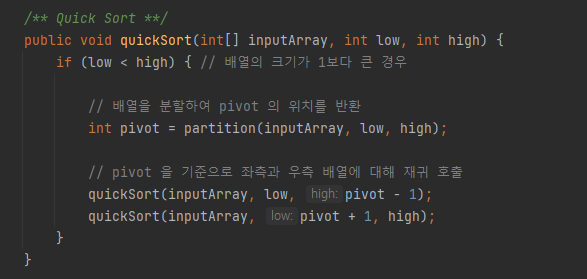
다음은 퀵 정렬을 구현한 자바 코드 예시입니다. quickSort() 메서드에서는 정렬 시킬 배열과 배열의 최소 최대 인덱스(low, high index)를 인자(Parameter)로 같이 넘겨줍니다. quickSort() 메서드에서는 다음 피벗을 리턴하는 partition()를 호출하고, 리턴 받은 피벗을 기준으로 분할된 좌측, 우측 배열을 재귀 호출합니다.

partition() 메서드에서는 배열의 마지막 요소를 피벗으로 설정하고, 반복문으로 피벗보다 작은 요소는 좌측 부분 배열에 배치하고, 큰 요소는 우측 부분 배열에 배치합니다. 반복문이 끝나면 해당 피벗을 좌측 배열의 마지막, 즉 좌측 배열과 우측 배열의 사이에 위치 시켜 최종적인 위치를 확정합니다.

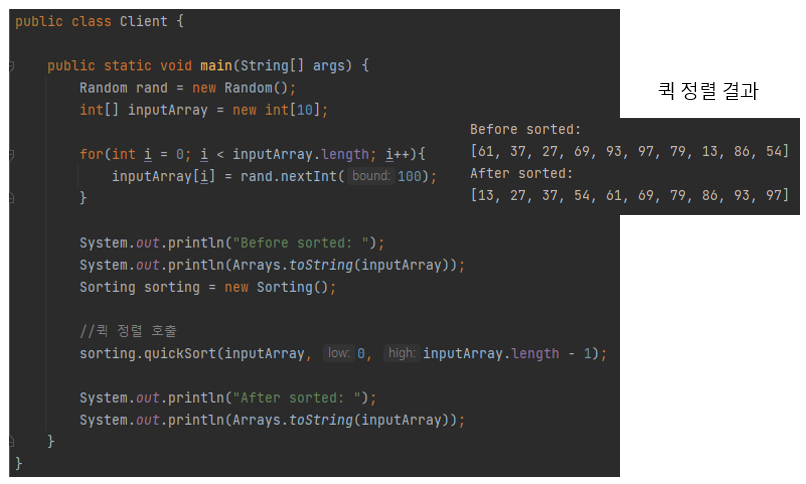
이제 클라이언트 코드에서 앞서 구현한 퀵 정렬을 실행합니다. 그러면 다음 그림과 같이 퀵 정렬도 정상적으로 동작하는 것을 살펴볼 수 있습니다.

각 정렬 알고리즘 시간 복잡도 비교 분석

1) 시간 복잡도 분석

시간 복잡도는 알고리즘의 효율성을 측정하는 지표이며, 어떤 문제를 해결하는 데 어느 정도 시간이 걸리는지를 나타냅니다. 일반적으로 빅 오(Big O) 표기법으로 시간 복잡도를 표현하며, 입력 크기에 대한 함수로 나타냅니다.

F(n) = O(G(n))

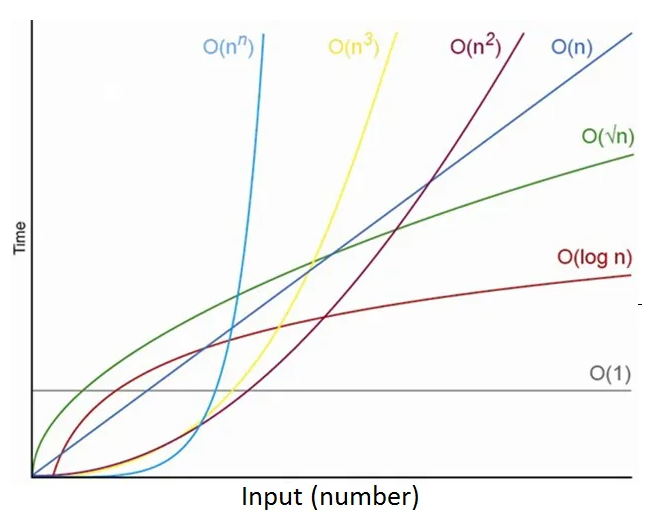
여기서 수학적으로 깊게 들어가면 조금 복잡해지지만, 간단하게 표현하자면 G(n)이 1차 다항식이면 O(n)으로 표기하고, 2차 다항식이면 O(n2)으로 표기합니다. 시간 복잡도는 아래 그림과 같이 O(1)이 가장 효율적이며, 다음으로 O(log n), O(n) 등이 따릅니다. O(n) 이후부터는 입력 크기가 커질수록 처리 시간이 급격히 늘기 때문에 비효율적인 알고리즘으로 여겨집니다.

2) 각 알고리즘의 시간 복잡도 비교

알고리즘 시간 복잡도는 최선(Best case), 최악(Worst case), 평균(Average case)으로 나눠서 분석할 수 있습니다. 삽입 정렬, 병합 정렬, 퀵 정렬에 대한 최선, 최악, 평균 시간 복잡도는 다음 표와 같습니다.

3) 장단점 및 사용 방법

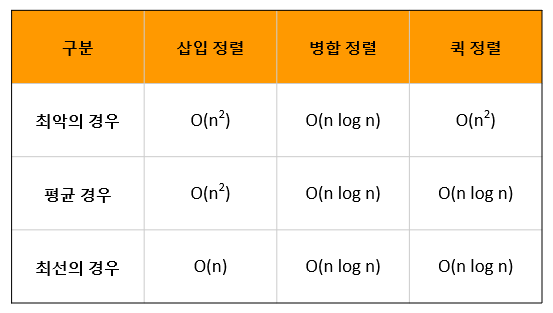
삽입 정렬은구현이 간단한정렬 알고리즘입니다. 하지만, 평균적으로 O(n2)의 시간 복잡도를 가지기 때문에 일반적으로 비효율적인 알고리즘이라고 할 수 있습니다. 따라서 삽입 정렬 알고리즘은 데이터셋이 극히 제한적인 경우 외에는 잘 사용하지 않습니다.

병합 정렬은 최악의 경우에도 어느 정도 성능을 보장하는 정렬 알고리즘입니다. 다만 부분 배열을 저장할 추가적인 메모리가 필요하므로, 데이터셋이 커질수록 공간 복잡도에 대한 고려가 필요합니다. 병합 정렬은 특별히 공간적인 부분에 문제가 없다면, 최악의 경우에도 좋은 성능을 보이기 위해 사용할 수 있습니다.

퀵 정렬은 병합 정렬과 달리 추가 메모리가 거의 필요하지 않습니다. 다만 최악의 경우 성능이 떨어질 수 있다는 단점이 있습니다. 따라서 메모리가 제한적인 환경에서 데이터셋이 너무 크지 않을 때 사용하는 것이 좋습니다.

마치며

지금까지 정렬 알고리즘 중 삽입 정렬, 병합 정렬, 퀵 정렬 알고리즘에 대해서 알아보고, 각 알고리즘의 시간 복잡도를 비교해 보았습니다. 정렬 알고리즘의 시간 복잡도에 대해 알고 있으면 특정 조건 하에 가장 적합한 알고리즘을 선택할 수 있으니, 각 알고리즘의 시간 복잡도 표는 어느 정도 암기해 두는 것이 좋습니다. 추가로, 위에서 살펴본 정렬 알고리즘 외에도 힙 정렬, 블록 병합 정렬,  인트로 정렬 같은 다양한 정렬 알고리즘도 있으니 참고하길 바랍니다.

요즘IT의 모든 콘텐츠는 저작권법의 보호를 받는 바, 무단 전재와 복사, 배포 등을 금합니다.