A/B 테스트 제대로 이해하기: 4 A/B 테스트 표본 크기와 유의미한 결과의 관계

바로 이전 글 에서 기초 통계 지식을 바탕으로 A/B 테스트 계산기의 세팅 방법과 해석에 관한 내용을 살펴보았다. 이때 해석 내용 중 계산기에서 ‘결과가 유의미하지 않다(Not Significant)’라고 했을 때 여러 변수가 생길 수 있다고 강조했다. 그래서 이번 글에서는 기획자와 PM, 마케터를 위해 ‘유의미하지 않은 결과’가 어떤 이유로 나온 것인지, 특히 ‘애초에 표본 사이즈와 유의미한 결과가 무슨 상관인지’를 알아보고자 한다.

표본(트래픽) 사이즈와 유의미한 결과가 무슨 상관이 있나요? 결론부터 말하면 아주 상관이 많다. 표본이 많으면 많을수록 그룹 A와 B의 결과 차이가 적더라도 '유의미하다'라고 인정해주기 때문이다.

그러면 왜 표본이 많으면 많을수록 작은 차이도 인정해주는 걸까?

우리의 생각1 “잘은 모르지만 표본은 많을수록 좋은 것 같다” 사실 ‘ 표본이 많을수록 좋다’는 이야기는 직관적으로 어느 정도 이해가 될 것 이다. 대통령 선거에서 미리 출구조사를 통해 A후보와 B후보의 투표율을 파악해서 누가 승리할지 짐작해보자고 하자. 전 국민에게 다 물어볼 순 없겠지만, 이왕이면 최대한 더 많은 사람에게 물어보면 신뢰할 수 있지 않겠는가?

투표를 마치고 온 주변 친구랑 가족 몇 명보다는 동네 사람들에게 물어보는 게 더 믿음이 갈 것이고, 동네 사람들보다는 전국의 투표소 앞에서 투표를 마친 이들을 붙잡고 물어보는 게 더 신뢰할 수 있을 것이다. 물론 가장 정확한 건 투표자 전체의 결과를 다 모아 보는 방식이지만, 이미 이건 추측이 아니라 전수 조사다.

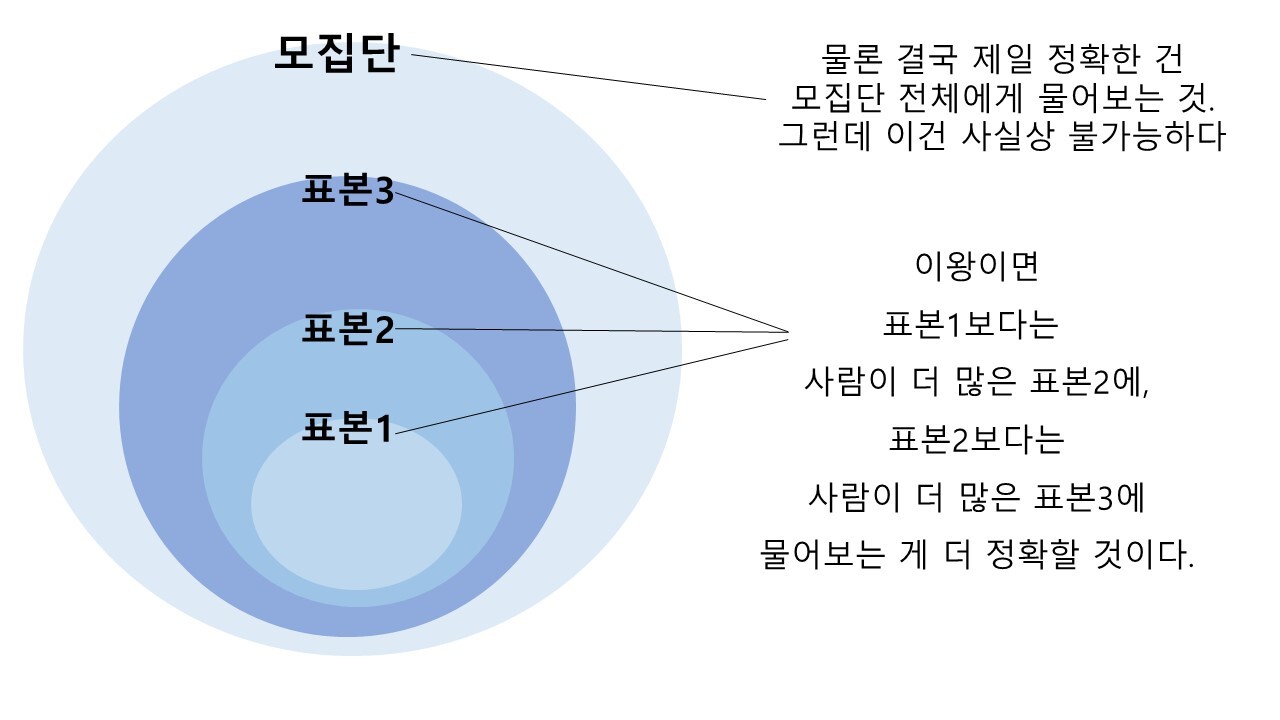
더 큰 표본에 물어볼수록 정확도는 높아지며, 가장 큰 표본은 결국 모집단 전체이다. 다만 모집단 전체에게 물어보는 건 매우 어렵거나 불가능하다.

그런데 표본이 많을수록 '더 적은 차이도 인정해준다'는 건 어떤 의미일까?

가상의 상황을 하나 생각해보자. A그룹은 전환율이 20%, B그룹은 전환율이 30%다. 얼핏 생각하면 무조건 B그룹이 승리한 것 같다.

그런데 만약 A그룹이 10명 중 2명, B그룹이 10명 중 3명이라면 우리는 이 결과를 신뢰할까? 다시 말해 '우연이 아니다'라고 생각할 수 있을까? 굳이 A/B 테스트 계산기를 돌려보지 않아도 우리의 직관은 이번 실험 결과가 그다지 유의미하지 않다고 판단할 것이다. 아무리 생각해도 그룹당 10명은 너무 적지 않은가? 그리고 전환율의 차이는 10%p라고 해도 결국 1명 차이 아닌가?

그럼 이번엔 전환율은 같은데 A그룹은 10,000명 중 2,000명, B그룹은 10,000명 중 3,000명이라면? 이럴 때도 역시나 A/B 테스트 계산기를 돌려보지 않아도 우리의 직관은 이번 실험 결과가 꽤 유의미할 거라고 느낄 것이다. 무려 각각 10,000명씩이나 트래픽을 모았으니까(= 조금 더 모집단에 가깝게, 많은 사람에게 물어봤으니까). 그리고 두 그룹의 결과 차이가 1,000명이나 되니까.

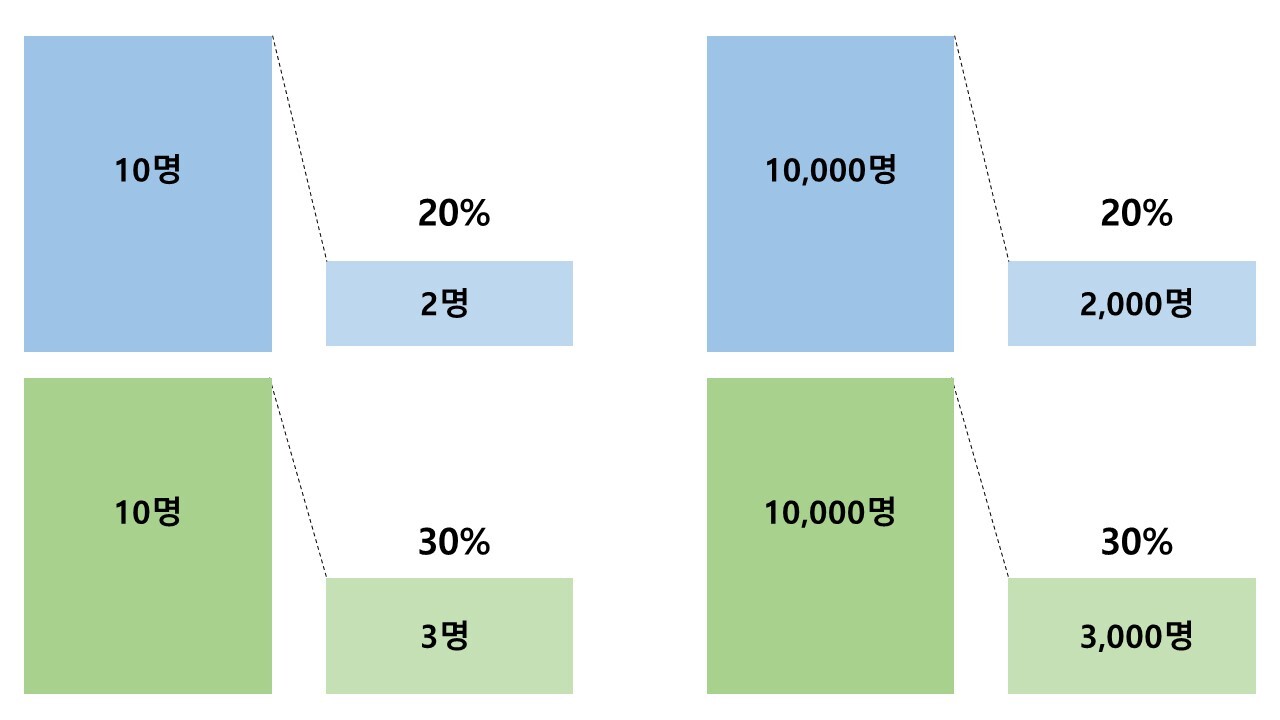
A/B 테스트 계산기를 돌려보지 않아도 우리는 왼쪽은 유의미하지 않고, 오른쪽은 유의미할 거라고 직감적으로 느낀다.

우리의 생각2 “차이가 커야 할 것 같은데, 이 트래픽에서 고작 이 정도 차이로 되나?” 자, 그럼 이번엔 아래의 경우를 살펴보자.

한 실험에선 좀 전과 같이 A그룹이 10,000명 중 2,000명이 전환에 성공하여 20% 전환율을, B그룹이 10,000명 중 3,000명이 전환에 성공하여 30% 전환율을 기록했다. 계산기는 안 돌려봤지만 충분히 유의미한 것 같다고 우리의 직관은 이야기한다.

그런데 다른 실험에선 트래픽을 훨씬 크게 키워서 A그룹은 100,000명 중 2,000명이 전환하여 2% 전환율을, B그룹은 100,000명 중 2,200명이 전환하여 2.2% 전환율을 기록했다. 이번엔 어떤 느낌이 드는가?

트래픽은 10배나 더 많다. 즉, 표본은 이전 실험보다 더 충분해졌다. (10,000명 → 100,000명) 그런데 전환율은 각각 2%와 2.2%로 훨씬 줄었다. 그리고 두 그룹의 전환율도 고작 0.2%p 차이로 훨씬 작아졌다 (10%p 차이 → 0.2%p 차이) 결국엔 두 그룹의 차이는 무려 100,000명 중에서 고작 200명 차이 아닌가? 이 정도 차이로 되나?

표본은 커졌지만 전환율과 두 그룹 간의 차이가 훨씬 적어졌다. 이런 경우, 직감적으로 실험 결과가 유의미하지 않게 느껴진다.

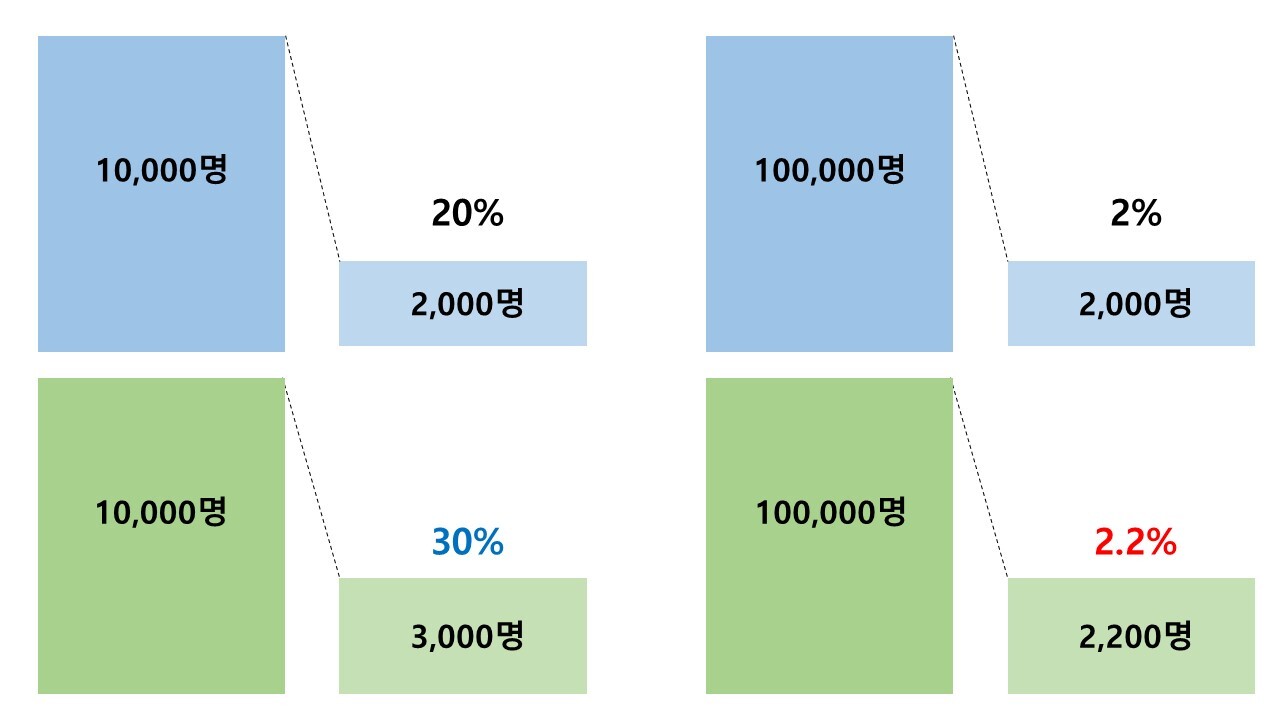
표본 크기와 A/B 테스트 결과의 차이에서 우리가 착각하는 것 앞에서 다음과 같이 가상의 세 결과를 살펴봤다.

실험1: 10명 중 2명 (20%) vs 10명 중 3명 (30%) 실험2: 10,000명 중 2,000명 (20%) vs 10,000명 중 3,000명 (30%) 실험3: 100,000명 중 2,000명 (2%) vs 100,000명 중 2,200명 (2.2%)

우리는 직감적으로 1) ‘표본이 클수록 결과가 유의미하다(우연이 아니다)’고 생각하고 2) 또한 ‘두 그룹 간의 결과 차이가 커야 유의미하다(우연이 아니다)’라고 생각한다. 그래서 우리는 실험1과 실험2 중에선 실험2가 더 낫다고 생각하지만, 반면 실험2와 실험3을 비교할 때는 아리송하게 느끼는 것이다. 그러나 실험3 결과 역시 신뢰 수준 95%의 양측 검정 기준으로 P-value가 0.0018로 유의미하다.

그러면 이쯤에선 이런 질문이 생긴다.

“아니, 100,000명 중 고작해야 2,000명 정도이고 두 그룹 간의 차이도 200명, 0.2%p밖에 안 나는데 어떻게 유의미한가요? 이 정도면 거의 차이가 없는 거 아닌가요?”

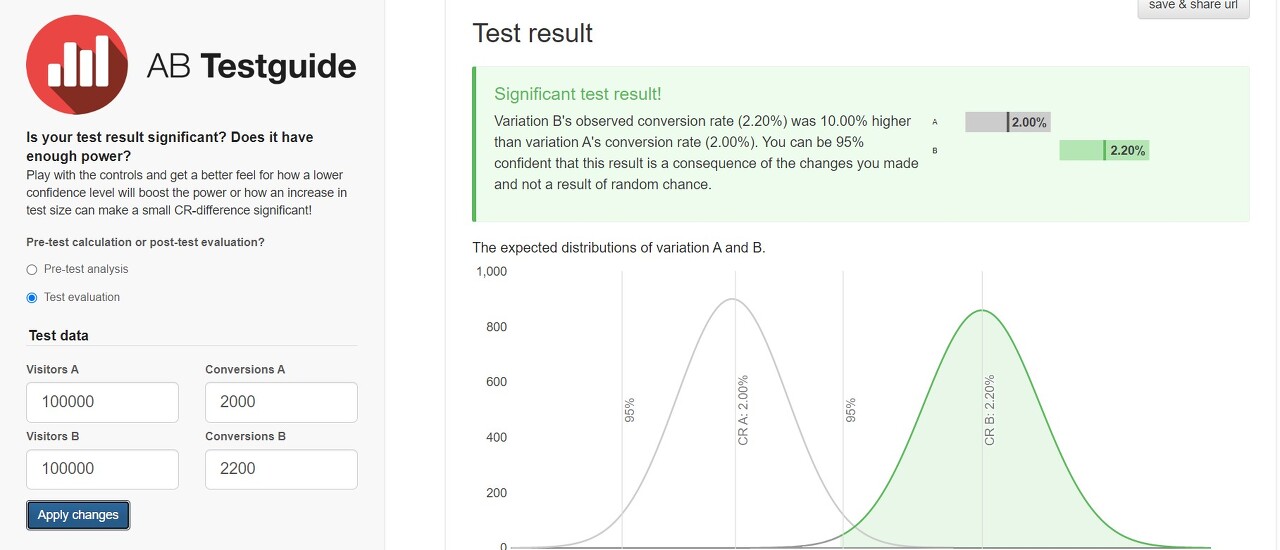
실험 3의 결과. 신뢰 수준 95%의 양측 검정에서 100,000명 중 전환율은 2% vs 2.2%로 200명 차이지만, 놀랍게도 결과는 유의미하다.

왜냐하면 우리가 이런 숫자를 두고 생각하는 방식은 '100,000명 중에서 차이가 고작 0.2%p 수준'이지만, 통계적으로는 '0.2%p 차이밖에 없더라도 표본이 100,000명이나 되니 이 정도면 충분하기에 우연이라고 볼 수 없다'라는 뜻이다.

우리의 직관: 100,000명끼리 비교해서 차이가 고작 0.2%p 수준이다.

VS

통계: 0.2%p 차이밖에 없더라도 표본이 100,000명이나 되니 이 정도면 충분하다 + 우연이라고 볼 수 없다.

즉, 아무리 차이가 적어 보이더라도 이건 100,000명을 대상으로 해서 얻은 실험 결과이니 통계적으로 충분히 유의미하다. 우리의 직관이 느낀 "100,000명 중에서 고작 차이가 이 정도밖에 안 되니 A와 B는 차이가 없다"는 잘못된 셈이다.

우리는 지금 단순히 비율을 비교하는 게 아니다. 우리는 이 비율의 차이가 정말로 믿을 수 있는 결과인지, 다른 경우에도 반복되어 우연이 아니란 걸 증명할 수 있는지 알고 싶은 거다. 표본이 커서 모집단의 크기에 가까워질수록 추측은 더욱 정확해지고, A와 B의 차이가 우연에 의해 발생할 가능성은 줄어든다.

우리는 단순히 비율을 비교하는 게 아니라 이 비율의 차이가 우연이 아닌지 알고 싶은 거다.

앞선 글에서 실험 결과가 유의미하지 않다고 했을 때, 두 가지 경우가 있는 걸 살펴봤다.

1) 애초에 두 그룹 사이에 별 차이가 없다.

2) 현재의 표본으로는 누가 더 낫거나 이번에만 우연한 결과인지 알 수 없다.

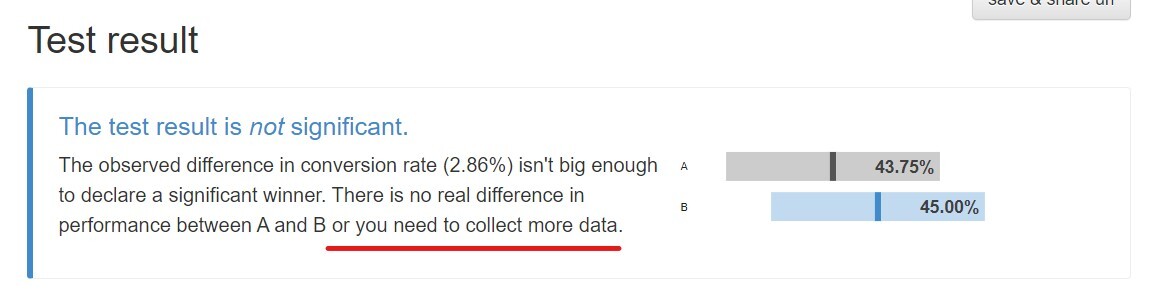
그리고 이번 글은 아래의 명제를 설명하기 위해 계속 이야기를 전개해왔다.

“표본이 크면 클수록 같거나 더 작은 차이로도 유의미하다는 평가를 얻어낼 수 있다”

결국, 이 명제는 ‘표본이 작으면 이 차이가 정말로 유의미한지, 우연이 아닌지 아직은 알 수 없지만, 표본만 충분하다면 판단해줄 수 있다’라는 의미이다. 더 나아가서는 ‘두 그룹의 차이가 똑같거나 심지어는 더 적더라도 두 그룹의 차이가 유의미하다고도 판단해줄 수도 있겠다’와 같은 뜻이다.

조금 더 쉽게 말하면, "두 그룹의 차이가 아무리 적어도 표본이 클수록 충분히 유의미할 수도 있다"는 이야기가 된다.

“두 그룹의 차이가 아무리 적어도 표본만 크면 충분히 유의미할 수도 있다”

표본은 얼마나 모아야 할까? 이렇게 A/B 테스트의 결과가 유의미하지 않다는 결과를 받았을 때 우리가 하게 되는 질문인 '표본의 크기와 결과의 유의미함 사이에 무슨 상관이 있는 건가?'에 대해 살펴봤다.

그럼 이쯤에서 A/B 테스트를 설계하는 기획자, PM, 마케터는 고민에 빠진다.

“그럼 대체 표본은 어느 정도가 필요한 건가?”

“이 정도 표본이라면 어느 정도 차이여야 유의미한 건가?”

그래서 다음 글이자 시리즈 마지막 편에서는 ‘A/B 테스트를 수행할 때 대체 표본(트래픽)은 얼마나 모아야 하는지?’와 ‘이와 관련해 테스트를 세팅, 실행할 때 주의할 점은 없는지?’에 관해 살펴보고자 한다.