집합의 관점에서 타입스크립트 바라보기

국내 유명 IT 기업은 한국을 넘어 세계를 무대로 할 정도로 뛰어난 기술과 아이디어를 자랑합니다. 이들은 기업 블로그를 통해 이러한 정보를 공개하고 있습니다. 요즘IT는 각 기업의 특색 있고 유익한 콘텐츠를 소개하는 시리즈를 준비했습니다. 이들은 어떻게 사고하고, 어떤 방식으로 일하는 걸까요?

이번 글은 국내 화장품 시장의 정보 비대칭 문제를 해결하고 소비자 중심의 뷰티 시장을 만들어 가고 있는 ‘화해’ 프론트엔드팀의 이야기입니다. 프론트엔드 영역에서 타입스크립트를 쓸 때 상식적으로 알고 있는 집합 관점에서 받아들이기 어려운 상황이 생깁니다. 왜 그런 상황이 생기는지 살펴보겠습니다.

안녕하세요. 버드뷰 개발팀 프론트엔드 플랫폼에서 화해 서비스를 만들고 있는 윤상호입니다.

요즘 프론트엔드 영역에서 타입스크립트를 쓰는 것은 선택이 아니라 필수로 자리 잡고 있습니다. 타입스크립트라는 이름에서부터 느낄 수 있듯이 타입을 작성하는 데에 시간을 많이 쏟고, 사용할 때는 타입을 집합의 관점에서 바라보고 사용하게 됩니다. 하지만 우리가 상식적으로 알고 있는 집합의 관점으로만 바라보기에는 받아들이기 어려운 상황이 발생합니다.

바로 아래처럼요.

keyof (A&B) = (keyof A) | (keyof B)
keyof (A|B) = (keyof A) & (keyof B)

우리가 알고 있는 합집합과 교집합의 개념이 유니온 타입과 구조적 타입에서 각각 다르기 때문입니다. 그 이유는 자바스크립트의 구조적 타이핑을 타입스크립트가 모델링했기 때문인데, 위 2줄의 코드가 왜 성립하는지 이해하기 어렵다면, 저와 함께 해석해보는 시간을 가져볼까요?

구조적 타이핑

당장 집합 이야기를 하기 전에 앞서 말했던 자바스크립트의 특징인 구조적 타이핑(덕 타이핑이라는 이름으로 불리기도 합니다)에 대해 이해가 선행되어야 합니다.

코끼리를 만진 장님 이야기

‘코끼리와 장님’이라는 우화를 아시나요? 옛날 시각장애인 6명에게 코끼리를 보게 했습니다. 눈으로는 볼 수 없기에 가까이 다가가서 만져보라고 하죠. 이들에게 현자가 코끼리가 어떻게 느껴지는지 물어보니 다리를 만진 이는 코끼리가 기둥이라 하고, 코를 만진 이는 나뭇가지, 꼬리를 만진 이는 밧줄, 귀를 만진 이는 부채, 배를 만진 이는 벽, 상아를 만진 이는 딱딱한 파이프라고 대답했습니다. 그리고 각자 경험했던 것을 토대로 자신의 의견이 옳다고 싸웁니다.

그러자 현자가 말합니다. “여러분 모두 맞습니다. 하지만 이야기한 것이 모두 다른 것은 여러분들이 코끼리의 각기 다른 부위를 만졌기 때문입니다. 코끼리는 여러분이 언급한 모든 특성을 가지고 있습니다.”라고 말이죠.

위 이야기에서 시각장애인이 코끼리의 일부분을 만지고, 이를 통해 몇 가지 특징을 추출한 후 본인이 파악한 특징에 부합하면 내가 만지고 있는 대상은 코끼리라고 판단합니다. 개발자가 어떤 대상을 코드로 객체화할 때도 마찬가지 아닐까요? 개발자가 생각하는 타입의 대표적인 특징들을 뽑아서 이것들만 코드로 정의해 놓습니다. 하지만 실제 대상은 이보단 훨씬 많은 특징을 가지는 경우가 많죠.

이처럼 구조적 타이핑은 객체가 어떤 타입에 부합하는 최소한의 특징을 가지고 있다면, 그냥 그 타입에 해당하는 것이라고 간주하는 것입니다. 이는 자바스크립트의 중요한 특징 중 하나입니다.

“만약 어떤 새가 오리처럼 걷고, 헤엄치고, 
꽥꽥거리는 소리를 낸다면 나는 그 새를 오리라고 부를 것이다.”

그러면 실제 코드를 통해 확인해볼까요?

type Person = {
name: string;
birth: Date;
death?: Date;
}

const Gamora = {
 name: '가모라',
 birth: new Date('1900/11/24'),
 death: new Date('2018/05/31'),
 home: '제호베레이 행성'
}

function enterEarth(p: Person) {
 console.log('지구에는 외계인이 들어올 수 없어요!')
}

enterEarth(Gamora); // 오류 없음

Gamora가 Person 타입에서 정의된 속성도 물론 가지고 있지만, home이라는 속성을 추가로 가지고 있음에도 함수 enterEarth에서 파라미터 타입 체커를 통과해버립니다.

타입스크립트는 자바스크립트에서 구현된 구조적 타이핑 개념을 그대로 사용하기 때문에 그렇습니다.

타입을 집합의 관점에서 바라보기

1. 구조적 타입에서의 교집합(인터섹션, &)

interface Person {
 name: string;
}

interface Lifespan {
 birth: Date;
 death?: Date;
}

type PersonSpan = Person & Lifespan;

연산자는 두 타입의 인터섹션(intersection, 교집합)을 계산합니다.

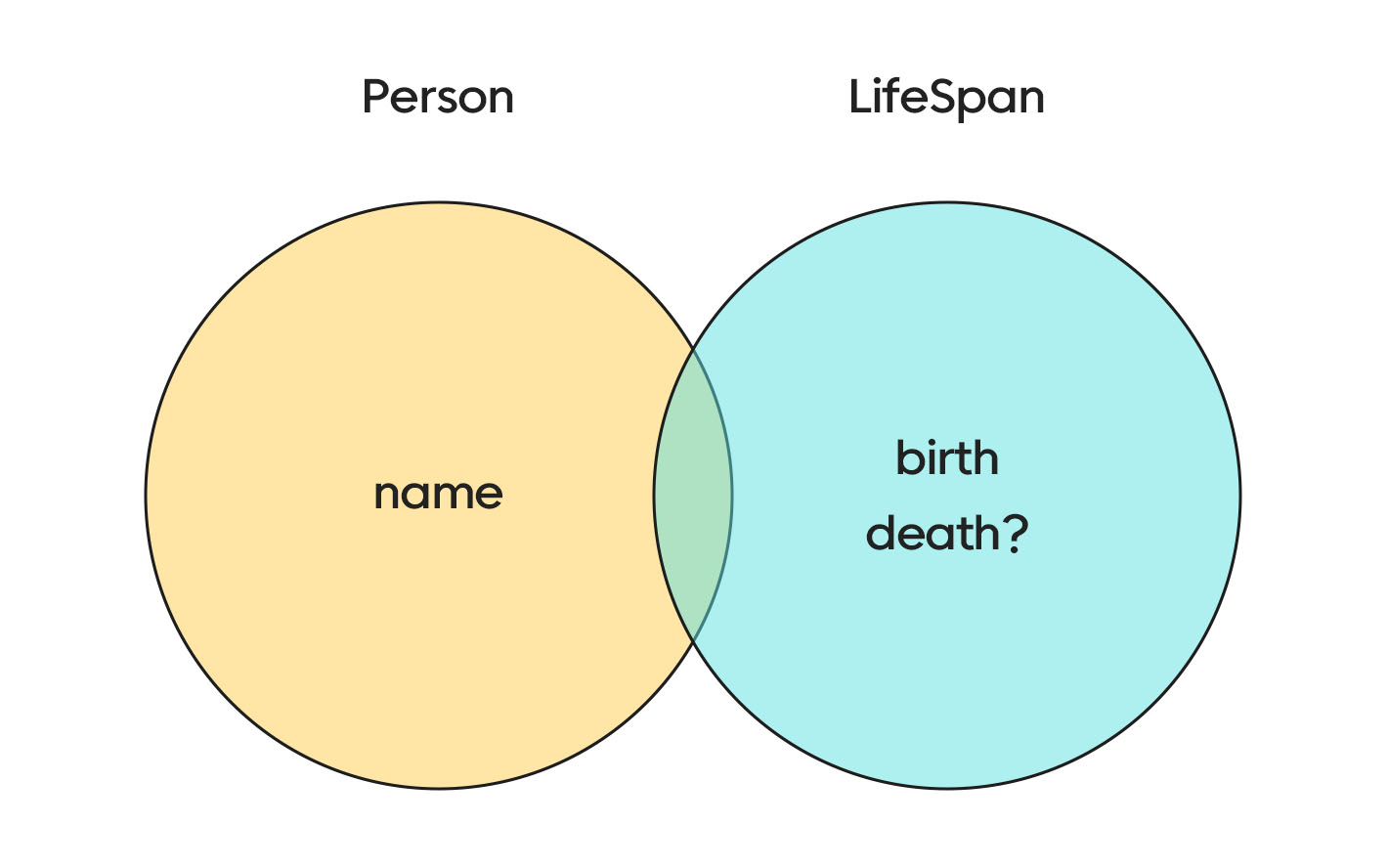
우리가 일반적으로 배워온 관점에 따르면 Person과 LifeSpan은 교집합이 없어 보입니다. 그러니 당연히 never가 나와야 하지 않을까요? 그러나 Person과 Lifespan을 둘 다 가지는 값은 인터섹션 타입에 속하게 됩니다.

여기서부터 혼란이 옵니다.

“never가 아니라고? 겹치는 것도 없는데?”

다시 생각해봅시다.

교집합이 되려면 그 교집합을 Person으로 간주해도, LifeSpan으로 간주해도 무리가 없어야 합니다. 즉, 타입관점에서 Person에도 속하고, Life에도 속하는 타입이 교집합이 되겠지요.

혹시 앞서 소개드렸던 내용이 하나 생각나지 않으십니까? 바로 구조적 타이핑!

type Intersection = {
		name: string;
		birth: Date;
		death?: Date;
}

Person에 있는 속성도 가지고 있으면서, Life에 있는 속성을 모두 가지고 있어야 Person, Life 각각 간주해도 문제가 없을 것입니다. 왜요? 구조적 타이핑 때문이죠. 이제야 비로소 Type 관점에서의 ‘교집합’에 해당한다고 할 수 있겠습니다.

2. 유니온 타입

다시 앞선 코드를 가져와보겠습니다.

 name: string;
}

interface Lifespan {
 birth: Date;
 death?: Date;
}

참고

이건 어떻게 될까요?

type K = keyof (Person | LifeSpan);

K의 타입은 never가 됩니다. 혹시 K를 Person과 LifeSpan의 합집합이라고 생각하셨나요?

Person과 LifeSpan의 유니온 타입은 무슨 뜻일까요? 어떤 타입이 Person에 속하거나 아니면 LifeSpan 속해야 한다는 뜻이죠. 그런데 Person이거나 LifeSpan이 될 수 있는 속성이 아무것도 없습니다. 그러니 keyof를 한 결과가 never일 수밖에 없는 것입니다.

다른 예시를 들어볼까요?

type A = {
 a1: string;
 a2: string;
}

type B = {
	b1: string;
	b2: string;
}

keyof (A&B)는 어떻게 될까요?

keyof (A&B) = (keyof A) | (keyof B)

좌변부터 보겠습니다. 앞서 &는 인터섹션(교집합)이라고 배웠고, 이를 만족하는 타입은 결국 A와 B의 속성을 모두 가진 타입이라고 했습니다. A와 B의 모든 속성을 keyof 연산을 해보면, 좌변은 ‘a1’ | ‘a2’ | ‘b1’ | ‘b2’가 됩니다.

다음으로 우변을 보겠습니다. A의 keyof 연산의 결과는 ‘a1’ | ‘a2’입니다. B의 keyof 연산의 결과는 ‘b1’ | ‘b2’입니다. 그러면 이 둘의 유니온 타입은 ‘a1’ | ‘a2’ | ‘b1’ | ‘b2’가 되겠죠.

keyof (A|B) = (keyof A) & (keyof B)

이것도 좌변을 먼저 볼까요? 앞서 A|B의 keyof 연산 값이 never라고 했습니다. 우변을 보겠습니다. A의 keyof 연산의 결과는 ‘a1’ | ‘a2’입니다. B의 keyof 연산의 결과는 ‘b1’ | ‘b2’입니다. 이 둘은 겹치는 것이 없으니 never가 나와야겠죠.

3. 구조적 타이핑 관점에서 부분집합 바라보기

interface Vector1D { x: number; }
interface Vector2D { x: number; y: number; }
interface Vector3D { x: number; y: number; z: number; }

위 코드는 extends를 통해 똑같이 기능할 수 있습니다.

interface Vector1D { x: number; }
interface Vector2D extends Vector1D { y: number; }
interface Vector3D extends Vector2D { z: number; }

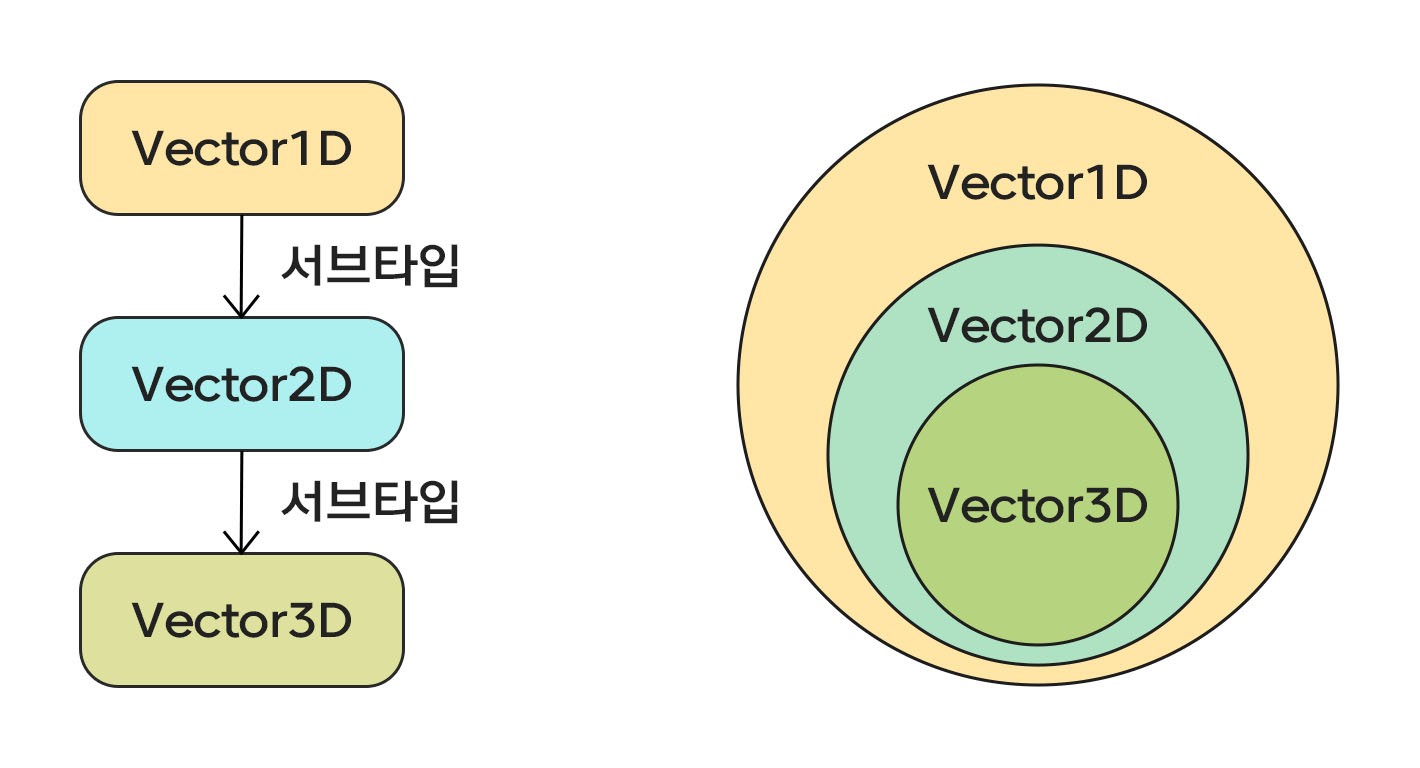
왜 Vector1D가 Vector2D를 포함하고 있는지, Vector2D가 Vector3D를 포함하고 있는지를 이해해봅시다.

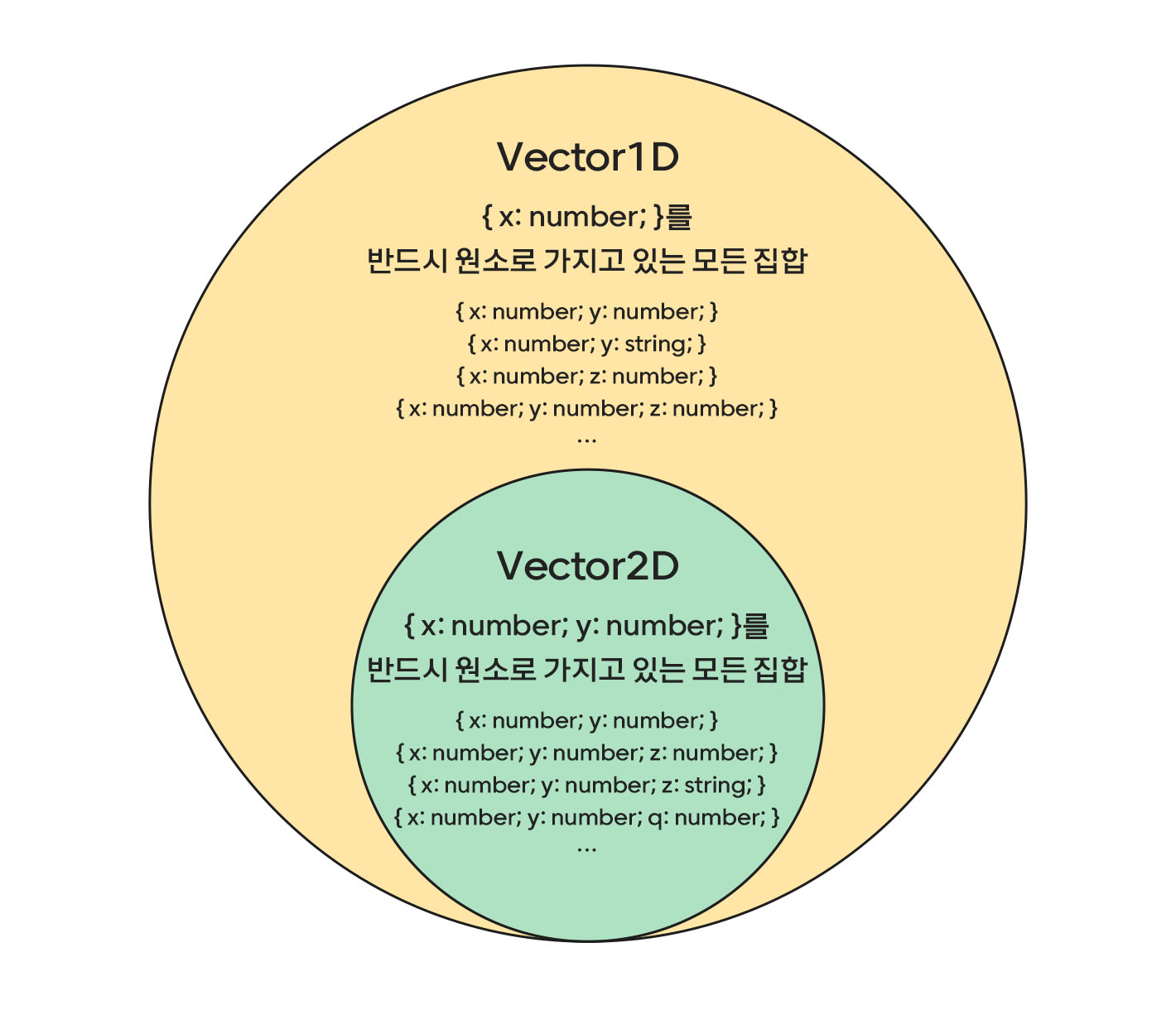
앞서 배운 구조적 타이핑 관점에서 바라보면 사실 Vector1D에 해당하는 집합(혹은 타입)의 개수는 무한합니다. 왜냐면 { x: number; }만 만족시키고, 이외에 추가적인 속성을 가져도 여전히Vector1D에 해당하기 때문이죠.

그 관점에서 Vector1D라는 타입 정의로 만들 수 있는 모든 경우의 타입(혹은 집합)에는 Vector2D로 만들 수 있는 모든 타입(혹은 집합) 또한 포함합니다. 당연히 Vector3D도 마찬가지입니다.

여기까지 오느라 수고 많으셨습니다. 타입스크립트에서 &와 |를 사용할 때는 두 가지만 기억하면 됩니다.

• 유니온 타입에서의 교집합, 합집합과 구조적 타입 { key: value }에서의 교집합, 합집합은 다르다.
• 그 이유는 자바스크립트의 구조적 타이핑을 타입스크립트가 모델링했기 때문이다.

읽어주셔서 감사합니다.

<원문>

집합의 관점에서 타입스크립트 바라보기